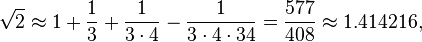Vedic mathematics were the first and foremost source of knowledge . Selflessly shared by Hindus to all around the world. The Hindu FAQs Will now answer some discoveries around the world which may have existed in vedic hindusim. And as i always say, We wont judge, We will just write the article, its you who should know whether to accept it or reject it. We Need open mind to read this article. Read and learn about our unbelievable history . It will blow your mind ! ! !
But first, let me state Stigler’s law of eponymy:
“No scientific discovery is named after its original discoverer.”
Funny isn’t it.
Well It is also claimed that Babylonians knew and used the rule of the right triangle Long before Bauhayana and Pythagoras. It is also claimet to be developed sometime before Euclid, and it’s displayed very well in Euclid’s Elements. Some claime that it was chinese who discovered it before anyone else.
Well I wont go with who discovere it first, Rather i would explain Bauhayana’s Theory as our website is to know about hinduism, and not to prove how to hinduism is greatest of all.
So, Baudhayana, (800 BCE) was the author of the Baudhayana sutras, which cover dharma, daily ritual, mathematics, etc. He belongs to the Yajurveda school, and is older than the other sutra author Apastamba.
He was the author of the earliest Sulba Sutra appendices to the Vedas giving rules for the construction of altars called the Baudhayana Sulbasutra. These are notable from the point of view of mathematics, for containing several important mathematical results, including giving a value of pi to some degree of precision, and stating a version of what is now known as the Pythagorean theorem.

Sequences associated with primitive Pythagorean triples have been named Baudhayana sequences. These sequences have been used in cryptography as random sequences and for the generation of keys.
Pythagorean Theorem
The square of the hypotenuse of a right-angled triangle equals to the sum of the square of the other two sides.
Baudhayana states:
“The area produced by the diagonal of a rectangle is equal to the sum of area produced by it on two sides.
Baudhayana listed Pythagoras theorem in his book called Baudhayana Sulbasutra (800 BCE). Incidentally, Baudhayana Sulbasûtra is also one of the oldest books on advanced Mathematics. The actual shloka (verse) in Baudhayana Sulbasutra that describes Pythagoras theorem is given below :
dirghasyaksanaya rajjuh parsvamani, tiryadam mani,
cha yatprthagbhute kurutastadubhayan karoti.
Interestingly, Baudhayana used a rope as an example in the above shloka which can be translated as – A rope stretched along the length of the diagonal produces an area which the vertical and horizontal sides make together. As you see, it becomes clear that this is perhaps the most intuitive way of understanding and visualizing Pythagoras theorem (and geometry in general) and Baudhāyana seems to have simplified the process of learning by encapsulating the mathematical result in a simple shloka in a layman’s language.

Some people might say that this is not really an actual mathematical proof of Pythagoras theorem though and it is possible that Pythagoras provided that missing proof. But if we look in the same Sulbasutra, we find that the proof of Pythagoras theorem has been provided by both Baudhayana and Apastamba in the Sulba Sutras! To elaborate, the shloka is to be translated as –
The diagonal of a rectangle produces by itself both (the areas) produced separately by its two sides.
Modern Pythagorean Theorem
The implications of the above statement are profound because it is directly translated into Pythagorean Theorem and it becomes evident that Baudhayana proved Pythagoras theorem. Since most of the later proofs are geometrical in nature, the Sulba Sutra’s numerical proof was unfortunately ignored. Though, Baudhayana was not the only Indian mathematician to have provided Pythagorean triplets and proof.
Apastamba also provided the proof for Pythagoras theorem, which again is numerical in nature but again unfortunately this vital contribution has been ignored and Pythagoras was wrongly credited by Cicero and early Greek mathematicians for this theorem.
Baudhayana also presented geometrical proof using isosceles triangles so, to be more accurate, we attribute the geometrical proof to Baudhayana and numerical (using number theory and area computation) proof to Apastamba. Also, another ancient Indian mathematician called Bhaskara later provided a unique geometrical proof as well as numerical which is known for the fact that it’s truly generalized and works for all sorts of triangles and is not incongruent (not just isosceles as in some older proofs).
Circling the square
Another problem tackled by Baudhayana is that of finding a circle whose area is the same as that of a square (the reverse of squaring the circle). His sutra i.58 gives this construction:
Draw half its diagonal about the centre towards the East-West line; then describe a circle together with a third part of that which lies outside the square.
Square root of 2
Baudhayana i.61-2 (elaborated in Apastamba Sulbasūtra i.6) gives the length of the diagonal of a square in terms of its sides, which is equivalent to a formula for the square root of 2:
samasya dvikarani. pramanam trityena vardhayet
tac caturthenatmacatustrimsonena savisesah.
The diagonal [lit. “doubler”] of a square. The measure is to be increased by a third and by a fourth decreased by the 34th. That is its diagonal approximately.
- The diagonal [lit. “doubler”] of a square. The measure is to be increased by a third and by a fourth decreased by the 34th. That is its diagonal approximately.
That is,
which is correct to five decimals.
Credits: Wiki
Disclaimer: All images, designs or videos in this page are copyright of their respective owners. We don’t own have these images/designs/videos. We collect them from search engine and other sources to be used as ideas for you. No copyright infringement is intended. If you have reason to believe that one of our content is violating your copyrights, please do not take any legal action as we are trying to spread the knowledge. You can contact us directly to be credited or have the item removed from the site.