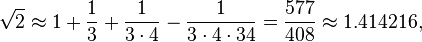Vedyske wiskunde wie de earste en wichtichste boarne fan kennis. Selsleas dield troch Hindoes oan oer de hiele wrâld. De Hindoe FAQ's sille no beantwurdzje op guon ûntdekkingen oer de hiele wrâld dy't mooglik bestien hawwe yn vedyske hindoesim. En lykas ik altyd sis, wy sille net oardielje, wy sille gewoan it artikel skriuwe, it is jo dy't moatte witte as jo it moatte akseptearje of ôfwize. Wy hawwe iepen geast nedich om dit artikel te lêzen. Lês en lear oer ús unbelievable skiednis. It sil jo geast blaze! ! !
Mar lit my earst Stigler's wet fan eponymy sizze:
"Gjin wittenskiplike ûntdekking is neamd nei syn oarspronklike ûntdekker."
Grappich is it net.
No It wurdt ek beweare dat Babyloniërs wisten en brûkten de regel fan 'e rjochte trijehoek Lang foar Bauhayana en Pythagoras. It wurdt ek beweare dat it ienris foar Euclid ûntwikkele is, en it wurdt heul goed werjûn yn Euclid's Elements. Guon beweare dat it Sinezen wie dy't it ûntdutsen foardat immen oars.
No, ik sil net gean mei wa't it earst ûntdekt, leaver soe ik de teory fan Bauhayana útlizze, om't ús webside is om te witten oer hindoeïsme, en net te bewizen hoe't hindoeïsme it grutste is fan alles.
Sa, Baudhayana, (800 f.Kr.) wie de skriuwer fan de Baudhayana sutras, dy't cover dharma, deistich ritueel, wiskunde, ensfh Hy heart ta de Yajurveda skoalle, en is âlder as de oare sutra skriuwer Apastamba.
Hy wie de skriuwer fan 'e ierste Sulba Sutra taheaksels oan' e Veda's dy't regels jouwe foar de bou fan alters neamd de Baudhayana Sulbasutra. Dizze binne opmerklik út it eachpunt fan 'e wiskunde, om't se ferskate wichtige wiskundige resultaten befetsje, wêrûnder it jaan fan in wearde fan pi ta in graad fan krektens, en it oanjaan fan in ferzje fan wat no bekend is as de Pythagoras-stelling.

Sequences ferbûn mei primitive Pythagorean triples binne neamd Baudhayana sekwinsjes. Dizze sekwinsjes binne brûkt yn kryptografy as willekeurige sekwinsjes en foar it generearjen fan kaaien.
Pythagorean Stelling
It kwadraat fan de hypotenusa fan in rjochthoekige trijehoek is lyk oan de som fan it kwadraat fan de oare twa kanten.
Baudhayana steaten:
"It gebiet produsearre troch de diagonaal fan in rjochthoek is lyk oan de som fan it gebiet dat oan twa kanten wurdt produsearre.
Baudhayana neamde Pythagoras teorem yn syn boek neamd Baudhayana Sulbasutra (800 f.Kr.). Trouwens, Baudhayana Sulbasûtra is ek ien fan 'e âldste boeken oer avansearre wiskunde. De eigentlike shloka (fers) yn Baudhayana Sulbasutra dy't Pythagoras stelling beskriuwt wurdt hjirûnder jûn:
dirghasyaksanaya rajjuh parsvamani, tiryadam mani,
cha yatprthagbhute kurutastadubhayan karoti.
Ynteressant brûkte Baudhayana in tou as foarbyld yn 'e boppesteande shloka dy't oerset wurde kin as - In tou spand oer de lingte fan' e diagonaal produseart in gebiet dat de fertikale en horizontale kanten tegearre meitsje. Sa't jo sjogge, wurdt it dúdlik dat dit faaks de meast yntuïtive manier is om Pythagoras-stelling te begripen en te visualisearjen (en mjitkunde yn 't algemien) en Baudhāyana liket it proses fan learen ferienfâldige te hawwen troch it wiskundige resultaat yn te kapseljen yn in ienfâldige shloka yn in lekentaal .

Guon minsken kinne sizze dat dit net echt in echt wiskundich bewiis is fan Pythagoras-stelling en it is mooglik dat Pythagoras dat ûntbrekkende bewiis levere. Mar as wy yn deselde Sulbasutra sjogge, fine wy dat it bewiis fan Pythagoras-stelling is levere troch sawol Baudhayana as Apastamba yn 'e Sulba Sutras! Om út te wreidzjen, moat de shloka oerset wurde as -
De diagonaal fan in rjochthoek produseart op himsels beide (de gebieten) dy't apart troch syn beide kanten produsearre wurde.
Moderne Pythagoras stelling
De gefolgen fan 'e boppesteande ferklearring binne djip, om't it direkt oerset is yn Pythagoras-stelling en it wurdt dúdlik dat Baudhayana de Pythagoras-stelling bewiisde. Om't de measte lettere bewizen geometrysk fan aard binne, waard it numerike bewiis fan 'e Sulba Sutra spitigernôch negearre. Hoewol, Baudhayana wie net de ienige Yndiaanske wiskundige dy't Pythagoreaanske trijelingen en bewiis levere hie.
Apastamba ek levere it bewiis foar Pythagoras stelling, dy't wer is numerike fan aard, mar wer spitigernôch dizze fitale bydrage is negearre en Pythagoras waard ferkeard byskreaun troch Cicero en iere Grykske wiskundigen foar dizze stelling.
Baudhayana presintearre ek geometrysk bewiis mei help fan gelykbenige trijehoeken, dus, om krekter te wêzen, skriuwe wy it geometryske bewiis oan Baudhayana en numerike (mei nûmerteory en gebietsberekkening) bewiis oan Apastamba. Ek in oare âlde Yndiaanske wiskundige neamd Bhaskara joech letter in unyk geometrysk bewiis as numerike dat bekend is om it feit dat it wirklik generalisearre is en wurket foar alle soarten trijehoeken en net ynkongruint is (net allinich isosceles lykas yn guon âldere bewizen).
Om it plein hinne
In oar probleem oanpakt troch Baudhayana is dat fan it finen fan in sirkel wêrfan it gebiet itselde is as dat fan in fjouwerkant (it tsjinoerstelde fan it kwadraatsjen fan de sirkel). Syn sutra i.58 jout dizze konstruksje:
Draw de helte fan syn diagonaal oer it sintrum rjochting de East-West line; beskriuw dan in sirkel tegearre mei in tredde part fan dat dat bûten it plein leit.
Fjouwerkante woartel fan 2
Baudhayana i.61-2 (útwurke yn Apastamba Sulbasūtra i.6) jout de lingte fan de diagonaal fan in fjouwerkant yn termen fan syn kanten, wat lykweardich is oan in formule foar de fjouwerkantswoartel fan 2:
samasya dvikarani. pramanam trityena vardhayet
tac caturthenatmacatustrimsonena savisesah.
De diagonaal [lit. "dûbelder"] fan in fjouwerkant. De maatregel moat mei in tredde ferhege wurde en mei in fjirde fermindere mei de 34e. Dat is syn diagonaal likernôch.
- De diagonaal [lit. "dûbelder"] fan in fjouwerkant. De maatregel moat mei in tredde ferhege wurde en mei in fjirde fermindere mei de 34e. Dat is syn diagonaal likernôch.
Dat is,
dat is goed oant fiif desimalen.
Credits: wiki
Disclaimer: Alle ôfbyldings, ûntwerpen of fideo's op dizze side binne copyright fan har respektive eigners. Wy hawwe dizze ôfbyldings / ûntwerpen / fideo's net. Wy sammelje se fan sykmasjine en oare boarnen om as ideeën foar jo te brûken. Gjin ynbreuk op auteursrjocht is bedoeld. As jo reden hawwe om te leauwen dat ien fan ús ynhâld jo auteursrjochten skeint, nim dan asjebleaft gjin juridyske aksje, om't wy besykje de kennis te fersprieden. Jo kinne direkt kontakt mei ús opnimme om byskreaun te wurden of it item fan 'e side te ferwiderjen.