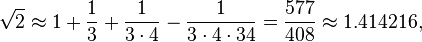वैदिक गणित ज्ञान का पहला और महत्वपूर्ण स्रोत था। निःस्वार्थ रूप से हिंदुओं द्वारा दुनिया भर में साझा किया गया। द हिंदू एफएक्यू अब दुनिया भर की कुछ खोजों का जवाब देगा, जो वैदिक हिंदू धर्म में मौजूद हो सकती हैं। और जैसा कि मैं हमेशा कहता हूं, हम अभिप्राय नहीं करेंगे, हम सिर्फ लेख लिखेंगे, आपको यह जानना चाहिए कि इसे स्वीकार करना चाहिए या अस्वीकार करना चाहिए। हमें इस लेख को पढ़ने के लिए खुले दिमाग की आवश्यकता है। हमारे अविश्वसनीय इतिहास के बारे में पढ़ें और जानें। इससे तुम्हारा दिमाग खुल जाएगा ! ! !
लेकिन पहले, मुझे स्टिग्लर के नाम के कानून का राज्य करने दें:
"कोई भी वैज्ञानिक खोज अपने मूल खोजकर्ता के नाम पर नहीं है।"
अजीब बात है ना।
वैसे यह भी दावा किया जाता है कि बाबुल के लोग बाऊहना और पाइथागोरस से बहुत पहले सही त्रिकोण के नियम को जानते थे और उसका इस्तेमाल करते थे। यह यूक्लिड से कुछ समय पहले विकसित होने का भी दावा है, और यह यूक्लिड के तत्वों में बहुत अच्छी तरह से प्रदर्शित होता है। कुछ लोगों का कहना है कि यह चीनी था जिसने इसे किसी और से पहले खोज लिया था।
वैसे मैं नहीं जानता कि यह पहले किसने खोजा था, बल्कि मैं बौहाना की थ्योरी समझाता हूं क्योंकि हमारी वेबसाइट हिंदुत्ववाद के बारे में जानने के लिए है, न कि यह साबित करने के लिए कि कैसे हिंदूवाद सबसे बड़ा है।
तो, बौधायन, (800 ईसा पूर्व) बौधायन सूत्र के लेखक थे, जो धर्म, दैनिक अनुष्ठान, गणित, आदि को कवर करते थे। वह यजुर्वेद विद्यालय से संबंधित हैं, और अन्य संत लेखक अपस्ताम्बा से बड़े हैं।
वे वेदों में सबसे प्राचीन सुल्बा सूत्र के लेखक थे, जिन्होंने वेधशालाओं के निर्माण के लिए नियम दिए, जिन्हें बौधायन सुल्बसुत्र कहा गया। ये गणित के दृष्टिकोण से उल्लेखनीय हैं, कई महत्वपूर्ण गणितीय परिणामों को शामिल करने के लिए, कुछ हद तक परिशुद्धता के लिए पीआई का मूल्य देना, और अब पाइथागोरस प्रमेय के रूप में जाना जाता है के एक संस्करण को बताते हुए।

आदिम पायथागॉरियन त्रिगुणों से जुड़े दृश्यों को बौधायन दृश्यों का नाम दिया गया है। इन अनुक्रमों का उपयोग क्रिप्टोग्राफी में यादृच्छिक अनुक्रमों और कुंजियों की पीढ़ी के लिए किया गया है।
पाइथागोरस प्रमेय
समकोण त्रिभुज के कर्ण का वर्ग अन्य दो भुजाओं के वर्ग के योग के बराबर होता है।
बौधायन राज्य:
“एक आयत के विकर्ण द्वारा निर्मित क्षेत्र दो तरफ से उत्पादित क्षेत्र के योग के बराबर है।
बौधायन ने पाइथागोरस प्रमेय को बौधायन सुलससूत्र (800 ईसा पूर्व) नामक अपनी पुस्तक में सूचीबद्ध किया। संयोग से, Baudhayana Sulbasallytra भी उन्नत गणित पर सबसे पुरानी पुस्तकों में से एक है। बौधायन सुलससूत्र में पाइथागोरस प्रमेय का वर्णन करने वाला वास्तविक श्लोक (पद्य) नीचे दिया गया है:
दिरघास्यकन्या रज्जु परस्वामनि, त्रयदम मणि,
च यत्प्रथगभूते कुरुतास्तदभयं करोति।
दिलचस्प बात यह है कि बौधायन ने उक्त श्लोक में एक उदाहरण के रूप में एक रस्सी का उपयोग किया था जिसका अनुवाद इस प्रकार किया जा सकता है - तिरछे की लंबाई के साथ खिंची गई रस्सी एक क्षेत्र का निर्माण करती है जिसे ऊर्ध्वाधर और क्षैतिज पक्ष एक साथ बनाते हैं। जैसा कि आप देख रहे हैं, यह स्पष्ट हो जाता है कि यह शायद पाइथागोरस प्रमेय (और सामान्य रूप से ज्यामिति) को समझने और देखने का सबसे सहज तरीका है और बौधायन ने एक आम आदमी की भाषा में एक सरल श्लोक में गणितीय परिणाम को संलग्न करके सीखने की प्रक्रिया को सरल बनाया है। ।

कुछ लोग कह सकते हैं कि यह वास्तव में पाइथागोरस प्रमेय का वास्तविक गणितीय प्रमाण नहीं है और यह संभव है कि पाइथागोरस ने उस लापता प्रमाण को प्रदान किया हो। लेकिन अगर हम एक ही सुल्बसुत्र में देखें, तो हम पाते हैं कि पाइथागोरस प्रमेय का प्रमाण सुलबा सूत्र में बौधायन और आपस्तंब दोनों द्वारा प्रदान किया गया है! विस्तृत करने के लिए श्लोक का अनुवाद करना है -
एक आयत का विकर्ण स्वयं दोनों (क्षेत्रों) दोनों पक्षों द्वारा अलग-अलग निर्मित होता है।
आधुनिक पायथागॉरियन प्रमेय
उपरोक्त कथन के निहितार्थ गहन हैं क्योंकि इसका सीधा अनुवाद पाइथोगोरियन प्रमेय में किया गया है और यह स्पष्ट हो जाता है कि बौधायन ने पाइथागोरस प्रमेय को सिद्ध कर दिया। चूँकि बाद के अधिकांश प्रमाण प्रकृति में ज्यामितीय हैं, इसलिए सुल्त सूत्र का संख्यात्मक प्रमाण दुर्भाग्य से अनदेखा कर दिया गया था। हालाँकि, बौधायन एकमात्र भारतीय गणितज्ञ नहीं थे जिन्होंने पाइथागोरस की त्रिक और प्रमाण प्रदान किए थे।
अपस्ताम्बा ने पाइथागोरस प्रमेय के लिए प्रमाण भी प्रदान किया, जो फिर से प्रकृति में संख्यात्मक है लेकिन दुर्भाग्य से इस महत्वपूर्ण योगदान को नजरअंदाज कर दिया गया है और पाइथागोरस को इस प्रमेय के लिए सिसरो और शुरुआती ग्रीक गणितज्ञों द्वारा गलत तरीके से श्रेय दिया गया था।
बौधायन ने समद्विबाहु त्रिभुजों का उपयोग करते हुए ज्यामितीय प्रमाण भी प्रस्तुत किया है, इसलिए अधिक सटीक होने के लिए, हम बौधायन और संख्यावाचक (संख्या सिद्धांत और क्षेत्र संगणना का उपयोग करते हुए) अपास्तम्बा को ज्यामितीय प्रमाण देते हैं। इसके अलावा, भास्कर नामक एक अन्य प्राचीन भारतीय गणितज्ञ ने बाद में एक अद्वितीय ज्यामितीय प्रमाण के साथ-साथ संख्यात्मक भी प्रदान किया, जो इस तथ्य के लिए जाना जाता है कि यह वास्तव में सामान्यीकृत है और सभी प्रकार के त्रिकोणों के लिए काम करता है और असंगत नहीं है (न केवल समद्विबाहु और कुछ पुराने प्रमाणों में)।
चौक का चक्कर लगाना
बौधायन से निपटने के लिए एक और समस्या है एक वृत्त की खोज करना जिसका क्षेत्रफल एक वर्ग के समान हो (चक्र के विपरीत भाग)। उनका सूत्र i.58 इस निर्माण को देता है:
पूर्व-पश्चिम रेखा की ओर केंद्र के बारे में इसका आधा विकर्ण ड्रा करें; फिर एक वृत्त का एक तिहाई भाग के साथ मिलकर वर्णन करें जो वर्ग के बाहर स्थित है।
2 का वर्गमूल
बौधायन i.61-2 (आपस्तम्बा सुलस्सुत्र i.6 में विस्तृत) अपने पक्षों के संदर्भ में एक वर्ग के विकर्ण की लंबाई देता है, जो 2 के वर्गमूल के लिए एक सूत्र के बराबर है:
समास्या द्विकारानी प्रणामं त्रितेना वर्धयेत्
tac caturthenatmacatustrimsonena सविसेह।
विकर्ण [जलाया] एक वर्ग का "डबललर"]। उपाय को एक तिहाई और एक चौथाई से 34 वें तक कम करना है। यह लगभग इसका विकर्ण है।
- विकर्ण [जलाया] एक वर्ग का "डबललर"]। उपाय को एक तिहाई और एक चौथाई से 34 वें तक कम करना है। यह लगभग इसका विकर्ण है।
यही कारण है,
जो पांच दशमलव तक सही है।
क्रेडिट: विकी
Disclaimer: इस पृष्ठ के सभी चित्र, डिज़ाइन या वीडियो उनके संबंधित स्वामियों के कॉपीराइट हैं। हमारे पास ये चित्र / डिज़ाइन / वीडियो नहीं हैं। हम उन्हें खोज इंजन और अन्य स्रोतों से इकट्ठा करते हैं जिन्हें आपके लिए विचारों के रूप में उपयोग किया जा सकता है। किसी कापीराइट के उलंघन की मंशा नहीं है। यदि आपके पास यह विश्वास करने का कारण है कि हमारी कोई सामग्री आपके कॉपीराइट का उल्लंघन कर रही है, तो कृपया कोई कानूनी कार्रवाई न करें क्योंकि हम ज्ञान फैलाने की कोशिश कर रहे हैं। आप हमसे सीधे संपर्क कर सकते हैं या साइट से हटाए गए आइटम को देख सकते हैं।