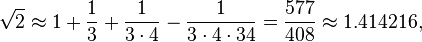വിജ്ഞാനത്തിന്റെ പ്രഥമവും പ്രധാനവുമായ ഉറവിടമായിരുന്നു വേദ ഗണിതം. ലോകമെമ്പാടുമുള്ള ഹിന്ദുക്കൾ നിസ്വാർത്ഥമായി പങ്കിട്ടു. ലോകമെമ്പാടുമുള്ള ചില കണ്ടുപിടുത്തങ്ങൾക്ക് ഹിന്ദു പതിവുചോദ്യങ്ങൾ ഇപ്പോൾ ഉത്തരം നൽകും. ഞാൻ എല്ലായ്പ്പോഴും പറയുന്നതുപോലെ, ഞങ്ങൾ വിധിക്കുകയില്ല, ഞങ്ങൾ ലേഖനം എഴുതുക, അത് സ്വീകരിക്കുകയോ നിരസിക്കുകയോ ചെയ്യണമെന്ന് നിങ്ങൾ അറിഞ്ഞിരിക്കണം. ഈ ലേഖനം വായിക്കാൻ ഞങ്ങൾക്ക് തുറന്ന മനസ്സ് ആവശ്യമാണ്. ഞങ്ങളുടെ അവിശ്വസനീയമായ ചരിത്രത്തെക്കുറിച്ച് വായിക്കുക, പഠിക്കുക. അത് നിങ്ങളുടെ മനസ്സിനെ blow തിക്കും! ! !

എന്നാൽ ആദ്യം, ഞാൻ സ്റ്റിഗ്ലറുടെ പേരിന്റെ നിയമം പ്രസ്താവിക്കട്ടെ:
“ശാസ്ത്രീയ കണ്ടെത്തലുകളൊന്നും അതിന്റെ യഥാർത്ഥ കണ്ടുപിടുത്തക്കാരന്റെ പേരില്ല.”
തമാശയല്ലേ.
ബ au ഹായാനയ്ക്കും പൈതഗോറസിനും വളരെ മുമ്പുതന്നെ ബാബിലോണിയക്കാർ ശരിയായ ത്രികോണത്തിന്റെ ഭരണം അറിയുകയും ഉപയോഗിക്കുകയും ചെയ്തുവെന്നും അവകാശപ്പെടുന്നു. യൂക്ലിഡിന് മുമ്പായി ഇത് വികസിപ്പിച്ചെടുക്കേണ്ട ക്ലെയിം കൂടിയാണ്, ഇത് യൂക്ലിഡിന്റെ ഘടകങ്ങളിൽ നന്നായി പ്രദർശിപ്പിക്കും. മറ്റാർക്കും മുമ്പായി ഇത് കണ്ടെത്തിയത് ചൈനക്കാരാണെന്ന് ചില അവകാശവാദങ്ങൾ.

ആദ്യം ഇത് കണ്ടെത്തിയവരുമായി ഞാൻ പോകില്ല, മറിച്ച് ഞങ്ങളുടെ വെബ്‌സൈറ്റ് ഹിന്ദുമതത്തെക്കുറിച്ച് അറിയുകയെന്നതാണ്, മാത്രമല്ല ഹിന്ദുമതം എങ്ങനെ മഹത്തരമാണെന്ന് തെളിയിക്കരുത് എന്നതും ഞാൻ ബ au ഹായാനയുടെ സിദ്ധാന്തം വിശദീകരിക്കും.

അതിനാൽ, ധർമ്മം, ദൈനംദിന ആചാരങ്ങൾ, ഗണിതശാസ്ത്രം മുതലായവ ഉൾക്കൊള്ളുന്ന ബ ud ധ്യന സൂത്രങ്ങളുടെ രചയിതാവായിരുന്നു ബ ud ദയാന, (അദ്ദേഹം ക്രി.മു. 800) യജുർവേദ സ്കൂളിൽ നിന്നുള്ളയാളാണ്, മറ്റ് സൂത്ര എഴുത്തുകാരനായ അപസ്താംബയേക്കാൾ പഴയയാളാണ് അദ്ദേഹം.
ബ ud ദയാന സുൽബസൂത്ര എന്നറിയപ്പെടുന്ന ബലിപീഠങ്ങളുടെ നിർമ്മാണത്തിന് നിയമങ്ങൾ നൽകുന്ന വേദങ്ങളുടെ ആദ്യകാല സുൽബ സൂത്ര അനുബന്ധങ്ങളുടെ രചയിതാവായിരുന്നു അദ്ദേഹം. ഗണിതശാസ്ത്രത്തിന്റെ വീക്ഷണകോണിൽ നിന്ന് ഇവ ശ്രദ്ധേയമാണ്, പൈയുടെ മൂല്യം ഒരു പരിധിവരെ കൃത്യതയോടെ നൽകുകയും പൈതഗോറിയൻ സിദ്ധാന്തം എന്നറിയപ്പെടുന്നതിന്റെ ഒരു പതിപ്പ് പ്രസ്താവിക്കുകയും ചെയ്യുന്നതുൾപ്പെടെ നിരവധി പ്രധാനപ്പെട്ട ഗണിത ഫലങ്ങൾ ഉൾക്കൊള്ളുന്നു.

പ്രാകൃത പൈതഗോറിയൻ ട്രിപ്പിളുകളുമായി ബന്ധപ്പെട്ട സീക്വൻസുകൾക്ക് ബ ud ദയാന സീക്വൻസുകൾ എന്ന് നാമകരണം ചെയ്തിട്ടുണ്ട്. ക്രിപ്റ്റോഗ്രഫിയിൽ റാൻഡം സീക്വൻസുകളായും കീകളുടെ ജനറേഷനായും ഈ സീക്വൻസുകൾ ഉപയോഗിച്ചു.

പൈത്തഗോറസ് സിദ്ധാന്തം
ഒരു വലത് കോണാകൃതിയിലുള്ള ത്രികോണത്തിന്റെ ഹൈപ്പോടെൻസസിന്റെ ചതുരം മറ്റ് രണ്ട് വശങ്ങളുടെ ചതുരത്തിന്റെ ആകെത്തുകയ്ക്ക് തുല്യമാണ്.

ബ ud ധ്യാന സംസ്ഥാനങ്ങൾ:
“ഒരു ദീർഘചതുരത്തിന്റെ ഡയഗണൽ ഉൽ‌പാദിപ്പിക്കുന്ന വിസ്തീർണ്ണം രണ്ട് വശങ്ങളിൽ ഉൽ‌പാദിപ്പിക്കുന്ന വിസ്തീർണ്ണത്തിന് തുല്യമാണ്.

ബ ud ധ്യാന തന്റെ പുസ്തകത്തിൽ പൈതഗോറസ് സിദ്ധാന്തത്തെ പട്ടികപ്പെടുത്തി. ആകസ്മികമായി, നൂതന ഗണിതശാസ്ത്രത്തിലെ ഏറ്റവും പഴയ പുസ്തകങ്ങളിലൊന്നാണ് ബ ud ധ്യാന സുൽബാസത്ര. പൈതഗോറസ് സിദ്ധാന്തത്തെ വിവരിക്കുന്ന ബ ud ധ്യാന സുൽബസൂത്രയിലെ യഥാർത്ഥ ശ്ലോക (വാക്യം) ചുവടെ കൊടുത്തിരിക്കുന്നു:

ദിർഗസ്യക്ഷണായ രജ്ജുh പാർശ്വമണി, തിര്യടം മണി,
ച യത്പാർത്ഥാഗ്ഭൂതേ കുരുതസ്തദുഭയാൻ കരോതി.

രസകരമെന്നു പറയട്ടെ, മുകളിലുള്ള ശ്ലോകയിൽ ബ ud ദയാന ഒരു കയർ ഉപയോഗിച്ചു, ഇതിനെ വിവർത്തനം ചെയ്യാൻ കഴിയും - ഡയഗോണലിന്റെ നീളത്തിൽ നീട്ടിയ ഒരു കയർ ലംബവും തിരശ്ചീനവുമായ വശങ്ങൾ ഒന്നിച്ച് നിർമ്മിക്കുന്ന ഒരു പ്രദേശം ഉൽ‌പാദിപ്പിക്കുന്നു. പൈതഗോറസ് സിദ്ധാന്തത്തെ (പൊതുവായി ജ്യാമിതിയും) മനസ്സിലാക്കുന്നതിനും ദൃശ്യവൽക്കരിക്കുന്നതിനുമുള്ള ഏറ്റവും അവബോധജന്യമായ മാർഗ്ഗമാണിതെന്ന് നിങ്ങൾ കാണുന്നത് പോലെ, ഗണിതശാസ്ത്ര ഫലത്തെ ഒരു സാധാരണക്കാരന്റെ ഭാഷയിൽ ലളിതമായ ഒരു ശ്ലോകത്തിൽ ഉൾപ്പെടുത്തിക്കൊണ്ട് ബ ud ദ്ധയാന പഠന പ്രക്രിയയെ ലളിതമാക്കിയതായി തോന്നുന്നു. .

ഇത് ശരിക്കും പൈതഗോറസ് സിദ്ധാന്തത്തിന്റെ യഥാർത്ഥ ഗണിതശാസ്ത്ര തെളിവല്ലെന്ന് ചിലർ പറഞ്ഞേക്കാം, കൂടാതെ പൈതഗോറസ് ആ നഷ്‌ടമായ തെളിവ് നൽകിയതാകാം. എന്നാൽ ഒരേ സുൽബസൂത്രത്തിൽ നോക്കിയാൽ, പൈതഗോറസ് സിദ്ധാന്തത്തിന്റെ തെളിവ് സൽബ സൂത്രങ്ങളിൽ ബ ud ധ്യാനയും അപസ്താംബയും നൽകിയിട്ടുണ്ടെന്ന് നമുക്ക് കാണാം! വിശദമായി പറഞ്ഞാൽ, ശ്ലോകയെ ഇനിപ്പറയുന്നതായി വിവർത്തനം ചെയ്യണം -
ഒരു ദീർഘചതുരത്തിന്റെ ഡയഗണൽ അതിന്റെ രണ്ട് വശങ്ങളും പ്രത്യേകം ഉൽ‌പാദിപ്പിക്കുന്ന രണ്ട് പ്രദേശങ്ങളും സ്വയം ഉത്പാദിപ്പിക്കുന്നു.

ആധുനിക പൈതഗോറിയൻ സിദ്ധാന്തം
മേൽപ്പറഞ്ഞ പ്രസ്‌താവനയുടെ അർത്ഥം അഗാധമാണ്, കാരണം ഇത് പൈതഗോറിയൻ സിദ്ധാന്തത്തിലേക്ക് നേരിട്ട് വിവർത്തനം ചെയ്യപ്പെട്ടിട്ടുണ്ട്, കൂടാതെ പൈധഗോറസ് സിദ്ധാന്തം ബ ud ധ്യാന തെളിയിച്ചതായി വ്യക്തമാണ്. പിന്നീടുള്ള മിക്ക തെളിവുകളും ജ്യാമിതീയ സ്വഭാവമുള്ളതിനാൽ, സുൽബ സൂത്രത്തിന്റെ സംഖ്യാ തെളിവ് നിർഭാഗ്യവശാൽ അവഗണിക്കപ്പെട്ടു. എന്നിരുന്നാലും, പൈതഗോറിയൻ ത്രിമൂർത്തികളും തെളിവുകളും നൽകിയ ഒരേയൊരു ഇന്ത്യൻ ഗണിതശാസ്ത്രജ്ഞൻ ബ ud ദയാന മാത്രമല്ല.

പൈതഗോറസ് സിദ്ധാന്തത്തിന് തെളിവും അപസ്താംബ നൽകിയിട്ടുണ്ട്, ഇത് വീണ്ടും സാംഖിക സ്വഭാവമുള്ളതാണ്, പക്ഷേ നിർഭാഗ്യവശാൽ ഈ സുപ്രധാന സംഭാവന അവഗണിക്കപ്പെട്ടു, ഈ സിദ്ധാന്തത്തിന് പൈതഗോറസ് സിസറോയും ആദ്യകാല ഗ്രീക്ക് ഗണിതശാസ്ത്രജ്ഞരും തെറ്റായി ക്രെഡിറ്റ് ചെയ്തു.

ഐസോസിലിസ് ത്രികോണങ്ങൾ ഉപയോഗിച്ച് ജ്യാമിതീയ തെളിവുകളും ബ ud ദയാന അവതരിപ്പിച്ചു, അതിനാൽ കൂടുതൽ കൃത്യമായി പറഞ്ഞാൽ, ജ്യാമിതീയ തെളിവ് ഞങ്ങൾ ബ ud ധ്യാനയ്ക്കും അക്കങ്ങളുടെ (നമ്പർ തിയറിയും ഏരിയ കണക്കുകൂട്ടലും ഉപയോഗിച്ച്) തെളിവും അപസ്താംബയ്ക്ക് നൽകുന്നു. ഭാസ്‌കര എന്ന മറ്റൊരു പുരാതന ഇന്ത്യൻ ഗണിതശാസ്ത്രജ്ഞൻ പിന്നീട് ഒരു അദ്വിതീയ ജ്യാമിതീയ തെളിവും സംഖ്യയും നൽകി, ഇത് യഥാർത്ഥത്തിൽ സാമാന്യവൽക്കരിക്കപ്പെട്ടതാണെന്നും എല്ലാത്തരം ത്രികോണങ്ങൾക്കും വേണ്ടി പ്രവർത്തിക്കുന്നുവെന്നും ഇത് പൊരുത്തപ്പെടുന്നില്ലെന്നും (ചില പഴയ തെളിവുകളിൽ ഉള്ളതുപോലെ ഐസോസെല്ലുകൾ മാത്രമല്ല) അറിയപ്പെടുന്നു.

ചതുരം ചുറ്റുന്നു

ബ ud ദയാന കൈകാര്യം ചെയ്യുന്ന മറ്റൊരു പ്രശ്നം, ഒരു ചതുരത്തിന്റെ വിസ്തീർണ്ണത്തിന് തുല്യമായ ഒരു വൃത്തം കണ്ടെത്തുക എന്നതാണ് (സർക്കിളിനെ തരംതിരിക്കുന്നതിന്റെ വിപരീതം). അദ്ദേഹത്തിന്റെ സൂത്രം i.58 ഈ നിർമ്മാണം നൽകുന്നു:

കിഴക്ക്-പടിഞ്ഞാറ് രേഖയിലേക്ക് മധ്യഭാഗത്ത് അതിന്റെ പകുതി ഡയഗണൽ വരയ്ക്കുക; ചതുരത്തിന് പുറത്തുള്ളതിന്റെ മൂന്നാമത്തെ ഭാഗത്തിനൊപ്പം ഒരു വൃത്തത്തെ വിവരിക്കുക.

2 ന്റെ വർ‌ഗ്ഗ റൂട്ട്
ബ ud ദയാന i.61-2 (അപസ്താംബ സുൽബാസത്ര i.6 ൽ വിശദീകരിച്ചിരിക്കുന്നു) ഒരു ചതുരത്തിന്റെ ഡയഗണോണലിന്റെ ദൈർഘ്യം അതിന്റെ വശങ്ങളുടെ അടിസ്ഥാനത്തിൽ നൽകുന്നു, ഇത് 2 ന്റെ വർ‌ഗ്ഗമൂലിയുടെ സമവാക്യത്തിന് തുല്യമാണ്:

സമസ്യ ദ്വികരണി. പ്രമാണം തൃത്യേന വർധയേത്
ടാക് കതുർഥേനത്മകാതുസ്ട്രിംസോനേന സവിസേശ..

ഡയഗണൽ [ലിറ്റ്. ഒരു ചതുരത്തിന്റെ “ഇരട്ട”]. അളവ് മൂന്നിലൊന്നിലും നാലിലൊന്ന് 34 ലും കുറയ്ക്കണം. ഏകദേശം അതിന്റെ ഡയഗണൽ ആണ്.

ഡയഗണൽ [ലിറ്റ്. ഒരു ചതുരത്തിന്റെ “ഇരട്ട”]. അളവ് മൂന്നിലൊന്നിലും നാലിലൊന്ന് 34 ലും കുറയ്ക്കണം. ഏകദേശം അതിന്റെ ഡയഗണൽ ആണ്.

അതാണ്,

അത് അഞ്ച് ദശാംശത്തിലേക്ക് ശരിയാണ്.

കടപ്പാട്: വിക്കി

പുരാതന ഇന്ത്യൻ യു‌എഫ്‌ഒ

നിരാകരണം: ഈ പേജിലെ എല്ലാ ചിത്രങ്ങളും ഡിസൈനുകളും വീഡിയോകളും അതത് ഉടമസ്ഥരുടെ പകർപ്പവകാശമാണ്. ഞങ്ങൾക്ക് ഈ ചിത്രങ്ങൾ / ഡിസൈനുകൾ / വീഡിയോകൾ ഇല്ല. നിങ്ങൾ‌ക്കായി ആശയങ്ങളായി ഉപയോഗിക്കുന്നതിനായി തിരയൽ‌ എഞ്ചിനിൽ‌ നിന്നും മറ്റ് ഉറവിടങ്ങളിൽ‌ നിന്നും ഞങ്ങൾ‌ അവ ശേഖരിക്കുന്നു. പകർപ്പവകാശ ലംഘനമൊന്നും ഉദ്ദേശിച്ചിട്ടില്ല. ഞങ്ങളുടെ ഉള്ളടക്കങ്ങളിലൊന്ന് നിങ്ങളുടെ പകർപ്പവകാശം ലംഘിക്കുന്നുവെന്ന് വിശ്വസിക്കാൻ നിങ്ങൾക്ക് കാരണമുണ്ടെങ്കിൽ, ഞങ്ങൾ അറിവ് പ്രചരിപ്പിക്കാൻ ശ്രമിക്കുന്നതിനാൽ നിയമപരമായ നടപടികളൊന്നും സ്വീകരിക്കരുത്. ക്രെഡിറ്റ് ചെയ്യുന്നതിന് നിങ്ങൾക്ക് നേരിട്ട് ഞങ്ങളെ ബന്ധപ്പെടാം അല്ലെങ്കിൽ സൈറ്റിൽ നിന്ന് ഇനം നീക്കം ചെയ്യാം.