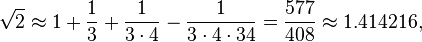ဝေဒသင်္ချာသည် အသိပညာ၏ ပထမနှင့် အရေးအကြီးဆုံး အရင်းအမြစ်ဖြစ်သည်။ ဟိန္ဒူဘာသာဖြင့် တစ်ကမ္ဘာလုံးသို့ ကိုယ်ကျိုးမဖက်ဘဲ မျှဝေပါသည်။ ဟိန္ဒူ FAQs များသည် ဝေဒဟိန္ဒူဘာသာတွင် တည်ရှိနေနိုင်သည့် ကမ္ဘာတစ်ဝှမ်းရှိ ရှာဖွေတွေ့ရှိမှုအချို့ကို ယခု အဖြေပေးပါမည်။ ငါအမြဲပြောသလိုပဲ၊ ငါတို့က အကဲဖြတ်မှာမဟုတ်ဘူး၊ ဆောင်းပါးကို လက်ခံမလား၊ ငြင်းပယ်မလားဆိုတာ သိသင့်တဲ့သူတွေပဲ ရေးမယ်။ ဒီဆောင်းပါးကိုဖတ်ဖို့ ပွင့်လင်းမြင်သာမှုရှိဖို့ လိုပါတယ်။ ကျွန်ုပ်တို့၏ မယုံနိုင်စရာသမိုင်းကြောင်းကို ဖတ်ရှုလေ့လာပါ။ မင်းစိတ်တွေ တုန်လှုပ်သွားလိမ့်မယ် ! ! !

ဒါပေမယ့် ဦးစွာပထမ၊ Stigler ရဲ့ ထင်ရှားကျော်ကြားတဲ့ ဥပဒေအကြောင်း ပြောပြပါရစေ။
"၎င်း၏မူရင်းရှာဖွေသူအား သိပ္ပံနည်းကျရှာဖွေတွေ့ရှိမှုဟူ၍ အမည်တပ်ထားခြင်းမရှိပါ။"
ရယ်စရာပဲ မဟုတ်လား။
Bauhyana နှင့် Pythagoras မတိုင်မီ ဗာဗုလုန်လူမျိုးများသည် ညာဘက်တြိဂံ၏ စည်းမျဉ်းကို ဟိုးရှေးရှေးကတည်းက သိရှိပြီး အသုံးပြုခဲ့သည်ဟုလည်း ဆိုထားသည်။ ၎င်းကို Euclid မတိုင်မီ တစ်ချိန်က တီထွင်ဖန်တီးခဲ့သည်ဟုလည်း ဆိုကြပြီး ၎င်းကို Euclid's Elements များတွင် အလွန်ကောင်းမွန်စွာ ပြသထားသည်။ အချို့က ၎င်းကို အခြားသူများမတိုင်မီ ရှာဖွေတွေ့ရှိခဲ့သည့် တရုတ်လူမျိုးများဖြစ်သည်ဟု ဆိုကြသည်။

အဲဒါကို ပထမဆုံးရှာတွေ့တဲ့ သူနဲ့ ကျွန်တော် မသွားဖြစ်ဘဲ၊ Bauhayana ရဲ့ သီအိုရီကို ကျွန်တော်တို့ ဝဘ်ဆိုဒ်က ဟိန္ဒူဘာသာအကြောင်း သိဖို့ဖြစ်ပြီး ဟိန္ဒူဘာသာက အကြီးမြတ်ဆုံးဆိုတာကို သက်သေပြဖို့မဟုတ်ဘဲ Bauhayana ရဲ့ Theory ကို ရှင်းပြမယ်။

ထို့ကြောင့်, Baudhayana, (800 BCE) သည်တရားဓမ္မ, နေ့စဉ်ထုံးတမ်း, သင်္ချာစသည်တို့ကိုဖုံးလွှမ်းထားတဲ့ Baudhayana သုတ္တန်ကိုရေးသားသူဖြစ်ပါတယ်။ သူသည် Yajurveda ကျောင်းပိုင်, နှင့်အခြားသုတ္တန်စာရေးဆရာ Apastamba ထက်အသက်ကြီးသည်။
သူသည် Baudhayana Sulbasutra ဟုခေါ်သော ယဇ်ပလ္လင်များဆောက်လုပ်ခြင်းအတွက် စည်းမျဉ်းများပေးဆောင်သည့် အစောဆုံး Sulba Sutra နောက်ဆက်တွဲများကို ရေးသားသူဖြစ်သည်။ ဤအရာများသည် သင်္ချာရှုထောင့်မှ မှတ်သားဖွယ်ရာများဖြစ်ပြီး၊ pi တန်ဖိုးကို တိကျမှုအတိုင်းအတာတစ်ခုအထိ ပေးဆောင်ခြင်းနှင့် ယခု Pythagorean သီအိုရီဟု ခေါ်ဝေါ်သည့် ဗားရှင်းတစ်ခုကို ဖော်ပြခြင်းအပါအဝင် အရေးကြီးသောသင်္ချာရလဒ်များပါရှိသည်။

ပဏာမ Pythagorean triple များနှင့်ဆက်စပ်သော sequence များကို Baudhayana sequences ဟုခေါ်သည်။ ဤ sequence များကို cryptography တွင် ကျပန်း sequence များ နှင့် keys များ ၏ မျိုးဆက်များအတွက် အသုံးပြုထားပါသည်။

Pythagorean သီအိုရီ
ညာထောင့်တြိဂံတစ်ခု၏ ဟိုက်တက်နုနပ်၏စတုရန်းသည် အခြားနှစ်ဘက်နှစ်ဘက်၏စတုရန်း၏ပေါင်းလဒ်နှင့်ညီမျှသည်။

Baudhayana က ဖော်ပြတယ်။:
“စတုဂံတစ်ခု၏ ထောင့်ဖြတ်ဖြင့် ဖြစ်ပေါ်လာသော ဧရိယာသည် နှစ်ဖက်ရှိ ၎င်းမှထွက်ရှိသော ဧရိယာပေါင်းလဒ်နှင့် ညီမျှသည်။

Baudhayana သည် သူ၏စာအုပ်တွင် Baudhayana Sulbasutra (800 BCE) တွင် Pythagoras သီအိုရီကို ဖော်ပြခဲ့သည်။ Baudhayana Sulbasûtra သည် အဆင့်မြင့်သင်္ချာဆိုင်ရာ ရှေးအကျဆုံးစာအုပ်များထဲမှ တစ်ခုလည်းဖြစ်သည်။ Pythagoras သီအိုရီကို ဖော်ပြသည့် Baudhayana Sulbasutra တွင် အမှန်တကယ် shloka (ပိုဒ်) ကို အောက်တွင် ဖော်ပြထားသည်။

dirghasyaksanaya rajjuh parsvamani, tiryadam mani၊
cha yatprthagbhute kurutastadubhayan karoti။

စိတ်ဝင်စားစရာမှာ Baudhayana သည် အထက်ပါ shloka တွင် ဘာသာပြန်ဆိုနိုင်သော ဥပမာတစ်ခုအနေဖြင့် - ထောင့်ဖြတ်မျဉ်း၏အလျားတစ်လျှောက် ဆန့်သောကြိုးသည် ဒေါင်လိုက်နှင့် အလျားလိုက်နှစ်ဖက်ပေါင်းစပ်ထားသည့် ဧရိယာကို ထုတ်ပေးသည်။ သင်မြင်သည့်အတိုင်း၊ ဤသည်မှာ Pythagoras သီအိုရီ (ယေဘုယျအားဖြင့် ဂျီသြမေတြီ) ကို နားလည်သဘောပေါက်ပြီး မြင်ယောင်ထင်မြင်နိုင်သော အလိုလိုသိမြင်နိုင်သောနည်းလမ်းဖြစ်ကောင်းဖြစ်နိုင်ကာ Baudhāyana သည် လူပြိန်းဘာသာစကားဖြင့် သင်္ချာရလဒ်ကို ရိုးရှင်းသော shloka တွင်ထည့်သွင်းခြင်းဖြင့် သင်ယူခြင်းလုပ်ငန်းစဉ်ကို ရိုးရှင်းစေပုံရသည်။ .

ဤသည်မှာ Pythagoras သီအိုရီ၏ တကယ့်သင်္ချာဆိုင်ရာ အထောက်အထားတစ်ခု မဟုတ်သော်လည်း Pythagoras သည် ထိုပျောက်ဆုံးနေသော အထောက်အထားကို ပေးစွမ်းနိုင်သည်ဟု အချို့က ဆိုနိုင်ပါသည်။ သို့သော် ကျွန်ုပ်တို့သည် တူညီသော Sulbasutra တွင်ကြည့်လျှင် Sulba Sutras တွင် Baudhayana နှင့် Apastamba နှစ်ခုစလုံးမှ Pythagoras သီအိုရီ၏ သက်သေအထောက်အထားကို Sulba Sutras တွင် ပေးဆောင်ထားကြောင်း တွေ့ရှိရသည်။ အတိအကျပြောရလျှင် shloka ကို-
စတုဂံတစ်ခု၏ ထောင့်ဖြတ်သည် နှစ်ဖက်စလုံးမှ သီးခြားထုတ်လွှတ်သော (ဧရိယာ) နှစ်ခုလုံးကို သူ့အလိုလို ထုတ်ပေးသည်။

ခေတ်သစ် Pythagorean သီအိုရီ
အထက်ပါဖော်ပြချက်၏ သက်ရောက်မှုများသည် Pythagorean Theorem သို့ တိုက်ရိုက်ပြန်ဆိုထားသောကြောင့် Baudhayana သည် Pythagoras သီအိုရီကို သက်သေပြခဲ့သည်မှာ ထင်ရှားပါသည်။ နောက်ပိုင်းအထောက်အထားအများစုသည် သဘာဝတွင် ဂျီဩမေတြီပုံစံဖြစ်သောကြောင့်၊ Sulba Sutra ၏ ကိန်းဂဏန်းအထောက်အထားများကို ကံမကောင်းစွာဖြင့် လျစ်လျူရှုခဲ့သည်။ သို့သော်၊ Baudhayana သည် Pythagorean triplets နှင့် အထောက်အထားများကို ပံ့ပိုးပေးသည့် အိန္ဒိယ သင်္ချာပညာရှင် တစ်ဦးတည်း မဟုတ်ပါ။

Apastamba သည် သဘာဝတွင် ကိန်းဂဏာန်းများဖြစ်သည့် Pythagoras သီအိုရီကိုလည်း သက်သေပြခဲ့သည်၊ သို့သော် ကံမကောင်းစွာဖြင့် ဤအရေးကြီးသောအလှူငွေကို လျစ်လျူရှုခဲ့ပြီး Pythagoras သည် ဤသီအိုရီအတွက် Cicero နှင့် ရှေးဂရိသင်္ချာပညာရှင်များမှ မှားယွင်းစွာဂုဏ်ပြုခဲ့သည်။

Baudhayana သည် isosceles တြိဂံများကို အသုံးပြု၍ ဂျီဩမေတြီဆိုင်ရာ အထောက်အထားကို တင်ပြခဲ့သည်၊ ထို့ကြောင့် ပိုမိုတိကျစေရန်အတွက်၊ ကျွန်ုပ်တို့သည် ဂျီဩမေတြီဆိုင်ရာ သက်သေကို Baudhayana နှင့် Apastamba သို့ ဂဏန်း (ဂဏန်းသီအိုရီနှင့် ဧရိယာတွက်ချက်ခြင်း) သက်သေအဖြစ် သတ်မှတ်ပေးပါသည်။ ထို့အပြင်၊ နောက်ပိုင်းတွင် Bhaskara ဟုခေါ်သော ရှေးခေတ်အိန္ဒိယသင်္ချာပညာရှင် မှ ထူးခြားသော ဂျီဩမေတြီဆိုင်ရာ အထောက်အထားအပြင် ၎င်းသည် အမှန်တကယ် ယေဘူယျအားဖြင့် တြိဂံအမျိုးအစားအားလုံးအတွက် အလုပ်လုပ်သည်ဟူသောအချက်ကြောင့် လူသိများသည့် ထူးခြားသည့် ဂျီဩမေတြီဆိုင်ရာ အထောက်အထားကို ပေးဆောင်ခဲ့ပြီး ကွဲလွဲမှုမရှိပါ (အချို့သော အထောက်အထားဟောင်းများတွင်ကဲ့သို့ အ isosceles မဟုတ်ပါ)။

ရင်ပြင်ကို လှည့်ပတ်သည်။

ဂေါတမဗုဒ္ဓက ကိုင်တွယ်ဖြေရှင်းသော နောက်ထပ်ပြဿနာတစ်ခုမှာ စတုရန်းတစ်ခု၏ ဧရိယာနှင့် တူညီသော စက်ဝိုင်းကို ရှာဖွေခြင်း (စက်ဝိုင်းကို နှစ်ထပ်ခွဲခြင်း၏ နောက်ပြန်ဆုတ်ခြင်း) ဖြစ်သည်။ သူ၏ သုတ္တန် i.58 သည် ဤတည်ဆောက်မှုကို ပေးသည်။

အရှေ့-အနောက်မျဉ်းဆီသို့ ဗဟိုမှ ၎င်း၏ထောင့်ဖြတ်တစ်ဝက်ကို ဆွဲပါ။ ထို့နောက် စတုရန်းအပြင်ဘက်တွင်ရှိသော သုံးပုံတစ်ပုံနှင့်အတူ စက်ဝိုင်းတစ်ခုကို ဖော်ပြပါ။

2 နှစ်ထပ်ကိန်း
Baudhayana i.61-2 (Apastamba Sulbasūtra i.6 တွင် အသေးစိပ်ဖော်ပြထားသည်) သည် ၎င်း၏ ဘေးနှစ်ဖက်အတွက် စတုရန်းတစ်ခု၏ ထောင့်ဖြတ်အလျားကို ပေးသည်၊၊

samasya dvikarani ။ pramanam trityena vardhayet
tac caturthenatmacatustrimsonena savisesah။

ထောင့်ဖြတ် [lit. စတုရန်းတစ်ခု၏ "နှစ်ဆ"] တိုင်းတာမှုသည် 34th ဖြင့် သုံးပုံတစ်ပုံနှင့် လေးပုံတစ်ပုံကို လျှော့ချရမည်ဖြစ်သည်။ ၎င်းသည် ခန့်မှန်းခြေအားဖြင့် ၎င်း၏ထောင့်ဖြတ်ဖြစ်သည်။

ထောင့်ဖြတ် [lit. စတုရန်းတစ်ခု၏ "နှစ်ဆ"] တိုင်းတာမှုသည် 34th ဖြင့် သုံးပုံတစ်ပုံနှင့် လေးပုံတစ်ပုံကို လျှော့ချရမည်ဖြစ်သည်။ ၎င်းသည် ခန့်မှန်းခြေအားဖြင့် ၎င်း၏ထောင့်ဖြတ်ဖြစ်သည်။

ဒါကဖြစ်ပါသည်,

၎င်းသည် ဒဿမငါးခု မှန်ကန်သည်။

ခရက်ဒစ်: ဝီကီ

ရှေးဟောင်း အိန္ဒိယ ပန်းကန်ပြားပျံ

ခွင: ဤစာမျက်နှာရှိ ပုံများ၊ ဒီဇိုင်းများ သို့မဟုတ် ဗီဒီယိုများအားလုံးသည် ၎င်းတို့၏ သက်ဆိုင်ရာပိုင်ရှင်များ၏ မူပိုင်ခွင့်ဖြစ်သည်။ ကျွန်ုပ်တို့တွင် ဤပုံများ/ဒီဇိုင်းများ/ဗီဒီယိုများ မရှိပါ။ သင့်အတွက် အကြံဥာဏ်များအဖြစ် အသုံးပြုရန်အတွက် ၎င်းတို့ကို ရှာဖွေရေးအင်ဂျင်နှင့် အခြားအရင်းအမြစ်များမှ စုဆောင်းပါသည်။ မူပိုင်ခွင့်ချိုးဖောက်ရန် ရည်ရွယ်ထားခြင်းမရှိပါ။ ကျွန်ုပ်တို့၏ အကြောင်းအရာတစ်ခုသည် သင်၏မူပိုင်ခွင့်များကို ချိုးဖောက်နေသည်ဟု ယုံကြည်ရန် အကြောင်းပြချက်ရှိပါက၊ ကျွန်ုပ်တို့သည် အသိပညာဖြန့်ဝေရန် ကြိုးစားနေသောကြောင့် မည်သည့်ဥပဒေကြောင်းအရ အရေးယူခြင်းမှ မပြုပါနှင့်။ ဘဏ်စာရင်းသွင်းရန် ကျွန်ုပ်တို့ထံ တိုက်ရိုက်ဆက်သွယ်နိုင်သည် သို့မဟုတ် ဤအရာကို ဝဘ်ဆိုက်မှ ဖယ်ရှားခိုင်းနိုင်သည်။