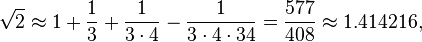A matemática védica foi a primeira e principal fonte de conhecimento. Abnegadamente compartilhado por hindus para todo o mundo. As Perguntas frequentes hindus agora responderão a algumas descobertas ao redor do mundo que podem ter existido no hindusim védico. E como eu sempre digo, não vamos julgar, vamos apenas escrever o artigo, é você quem deve saber se deve aceitá-lo ou rejeitá-lo. Precisamos de mente aberta para ler este artigo. Leia e aprenda sobre nossa história inacreditável. Isso vai explodir sua mente ! ! !
Mas primeiro, deixe-me declarar a lei de eponímia de Stigler:
“Nenhuma descoberta científica tem o nome de seu descobridor original.”
Engraçado não é.
Bem, também se afirma que os babilônios conheciam e usavam a regra do triângulo retângulo muito antes de Bauhayana e Pitágoras. Também é reivindicado para ser desenvolvido algum tempo antes de Euclides, e é exibido muito bem nos Elementos de Euclides. Alguns afirmam que foram os chineses que o descobriram antes de qualquer outra pessoa.
Bem, não irei com quem descobrir primeiro, em vez disso, explicaria a teoria de Bauhayana, pois nosso site é para saber sobre o hinduísmo, e não para provar como o hinduísmo é o maior de todos.
Então, Baudhayana, (800 aC) foi o autor dos sutras Baudhayana, que cobrem o dharma, ritual diário, matemática, etc. Ele pertence à escola Yajurveda e é mais antigo que o outro autor do sutra Apastamba.
Ele foi o autor dos primeiros apêndices do Sulba Sutra aos Vedas, dando regras para a construção de altares chamados de Baudhayana Sulbasutra. Estes são notáveis do ponto de vista da matemática, por conterem vários resultados matemáticos importantes, inclusive dando um valor de pi com algum grau de precisão, e estabelecendo uma versão do que hoje é conhecido como o teorema de Pitágoras.

As sequências associadas aos triplos pitagóricos primitivos foram denominadas sequências Baudhayana. Essas sequências têm sido utilizadas em criptografia como sequências aleatórias e para a geração de chaves.
Teorema de Pitágoras
O quadrado da hipotenusa de um triângulo retângulo é igual à soma do quadrado dos outros dois lados.
estados Baudhayana:
“A área produzida pela diagonal de um retângulo é igual à soma das áreas produzidas por ela em dois lados.
Baudhayana listou o teorema de Pitágoras em seu livro chamado Baudhayana Sulbasutra (800 aC). Aliás, Baudhayana Sulbasûtra é também um dos livros mais antigos de Matemática avançada. O shloka (verso) real em Baudhayana Sulbasutra que descreve o teorema de Pitágoras é dado abaixo:
dirghasyaksanaya rajjuh parsvamani, tiryadam mani,
cha yatprthagbhute kurutastadubhayan karoti.
Curiosamente, Baudhayana usou uma corda como exemplo no shloka acima, que pode ser traduzido como – Uma corda esticada ao longo do comprimento da diagonal produz uma área que os lados vertical e horizontal formam juntos. Como você vê, fica claro que esta é talvez a maneira mais intuitiva de entender e visualizar o teorema de Pitágoras (e a geometria em geral) e Baudhāyana parece ter simplificado o processo de aprendizado encapsulando o resultado matemático em um simples shloka na linguagem de um leigo .

Algumas pessoas podem dizer que esta não é realmente uma prova matemática real do teorema de Pitágoras e é possível que Pitágoras tenha fornecido a prova que faltava. Mas se olharmos no mesmo Sulbasutra, descobriremos que a prova do teorema de Pitágoras foi fornecida tanto por Baudhayana quanto por Apastamba nos Sulba Sutras! Para elaborar, o shloka deve ser traduzido como -
A diagonal de um retângulo produz por si mesma ambas (as áreas) produzidas separadamente por seus dois lados.
Teorema de Pitágoras Moderno
As implicações da afirmação acima são profundas porque ela é traduzida diretamente para o Teorema de Pitágoras e torna-se evidente que Baudhayana provou o teorema de Pitágoras. Como a maioria das provas posteriores são de natureza geométrica, infelizmente a prova numérica do Sulba Sutra foi ignorada. No entanto, Baudhayana não foi o único matemático indiano a fornecer trigêmeos e provas pitagóricas.
Apastamba também forneceu a prova para o teorema de Pitágoras, que novamente é de natureza numérica, mas novamente, infelizmente, esta contribuição vital foi ignorada e Pitágoras foi erroneamente creditado por Cícero e pelos primeiros matemáticos gregos por este teorema.
Baudhayana também apresentou prova geométrica usando triângulos isósceles, então, para ser mais preciso, atribuímos a prova geométrica a Baudhayana e a prova numérica (usando teoria dos números e computação de área) a Apastamba. Além disso, outro antigo matemático indiano chamado Bhaskara posteriormente forneceu uma prova geométrica única, bem como numérica, que é conhecida pelo fato de ser verdadeiramente generalizada e funcionar para todos os tipos de triângulos e não ser incongruente (não apenas isósceles como em algumas provas mais antigas).
circulando a praça
Outro problema abordado por Baudhayana é o de encontrar um círculo cuja área seja igual à de um quadrado (o inverso da quadratura do círculo). Seu sutra i.58 dá esta construção:
Desenhe metade de sua diagonal sobre o centro em direção à linha leste-oeste; em seguida, descreva um círculo junto com uma terça parte daquilo que está fora do quadrado.
Raiz quadrada de 2
Baudhayana i.61-2 (elaborado em Apastamba Sulbasūtra i.6) dá o comprimento da diagonal de um quadrado em termos de seus lados, o que é equivalente a uma fórmula para a raiz quadrada de 2:
samasya dvikarani. pramanam trityena vardhayet
tac caturthenatmacatustrimsonena savisesah.
A diagonal [lit. “dobrador”] de um quadrado. A medida deve ser aumentada em um terço e diminuída em um quarto até o 34º. Essa é a sua diagonal aproximadamente.
- A diagonal [lit. “dobrador”] de um quadrado. A medida deve ser aumentada em um terço e diminuída em um quarto até o 34º. Essa é a sua diagonal aproximadamente.
Isto é,
que está correto com cinco casas decimais.
créditos: Wiki
Aviso Legal: Todas as imagens, designs ou vídeos nesta página são direitos autorais de seus respectivos proprietários. Não possuímos essas imagens/designs/vídeos. Nós os coletamos do mecanismo de pesquisa e de outras fontes para serem usados como ideias para você. Nenhuma violação de direitos autorais é pretendida. Se você tiver motivos para acreditar que um de nossos conteúdos está violando seus direitos autorais, não tome nenhuma ação legal, pois estamos tentando espalhar o conhecimento. Você pode entrar em contato conosco diretamente para receber os créditos ou remover o item do site.