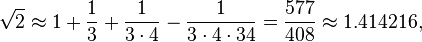Las matemáticas védicas fueron la primera y principal fuente de conocimiento. Desinteresadamente compartido por Hindus a todo el mundo. Las preguntas frecuentes hindúes ahora responderán algunos descubrimientos en todo el mundo que pueden haber existido en el hindusim védico. Y como siempre digo, no juzgaremos, solo escribiremos el artículo, eres tú quien debe saber si aceptarlo o rechazarlo. Necesitamos una mente abierta para leer este artículo. Lea y aprenda sobre nuestra increíble historia. Va a sorprenderte por completo ! ! !
Pero primero, permítanme enunciar la ley de eponimia de Stigler:
“Ningún descubrimiento científico lleva el nombre de su descubridor original”.
Gracioso ¿no?
Bueno, también se afirma que los babilonios conocían y usaban la regla del triángulo rectángulo mucho antes que Bauhayana y Pitágoras. También se afirma que se desarrolló en algún momento antes de Euclides, y se muestra muy bien en los Elementos de Euclides. Algunos aseguran que fueron los chinos quienes lo descubrieron antes que nadie.
Bueno, no iré con quién lo descubrió primero, sino que explicaría la Teoría de Bauhayana ya que nuestro sitio web es para saber sobre el hinduismo, y no para probar cómo el hinduismo es lo mejor de todo.
Entonces, Baudhayana, (800 a. C.) fue el autor de los sutras Baudhayana, que cubren el dharma, el ritual diario, las matemáticas, etc. Pertenece a la escuela Yajurveda y es más antiguo que el otro autor de sutra Apastamba.
Fue el autor de los primeros apéndices de Sulba Sutra a los Vedas que dan reglas para la construcción de altares llamados Baudhayana Sulbasutra. Estos son notables desde el punto de vista de las matemáticas, por contener varios resultados matemáticos importantes, incluido dar un valor de pi con cierto grado de precisión y establecer una versión de lo que ahora se conoce como el teorema de Pitágoras.

Las secuencias asociadas con los triples pitagóricos primitivos se han denominado secuencias de Baudhayana. Estas secuencias se han utilizado en criptografía como secuencias aleatorias y para la generación de claves.
Teorema de pitágoras
El cuadrado de la hipotenusa de un triángulo rectángulo es igual a la suma del cuadrado de los otros dos lados.
estados baudhayana:
“El área producida por la diagonal de un rectángulo es igual a la suma del área producida por él en dos lados.
Baudhayana enumeró el teorema de Pitágoras en su libro Baudhayana Sulbasutra (800 a. C.). Por cierto, Baudhayana Sulbasûtra es también uno de los libros más antiguos sobre matemáticas avanzadas. El shloka (verso) real en Baudhayana Sulbasutra que describe el teorema de Pitágoras se da a continuación:
dirghasyaksanaya rajjuh parsvamani, tiryadam mani,
cha yatprthagbhute kurutastadubhayan karoti.
Curiosamente, Baudhayana usó una cuerda como ejemplo en el shloka anterior que se puede traducir como: una cuerda estirada a lo largo de la diagonal produce un área que los lados verticales y horizontales forman juntos. Como puede ver, queda claro que esta es quizás la forma más intuitiva de comprender y visualizar el teorema de Pitágoras (y la geometría en general) y Baudhāyana parece haber simplificado el proceso de aprendizaje al encapsular el resultado matemático en un simple shloka en el lenguaje de un profano. .

Sin embargo, algunas personas podrían decir que esta no es realmente una prueba matemática real del teorema de Pitágoras y es posible que Pitágoras haya proporcionado esa prueba faltante. ¡Pero si miramos en el mismo Sulbasutra, encontramos que la prueba del teorema de Pitágoras ha sido proporcionada tanto por Baudhayana como por Apastamba en los Sulba Sutras! Para elaborar, el shloka debe traducirse como:
La diagonal de un rectángulo produce por sí misma ambas (las áreas) producidas separadamente por sus dos lados.
Teorema de Pitágoras moderno
Las implicaciones de la declaración anterior son profundas porque se traduce directamente al Teorema de Pitágoras y se hace evidente que Baudhayana demostró el teorema de Pitágoras. Dado que la mayoría de las pruebas posteriores son de naturaleza geométrica, desafortunadamente se ignoró la prueba numérica del Sulba Sutra. Sin embargo, Baudhayana no fue el único matemático indio que proporcionó pruebas y trillizos pitagóricos.
Apastamba también proporcionó la prueba del teorema de Pitágoras, que nuevamente es de naturaleza numérica, pero nuevamente, lamentablemente, esta contribución vital ha sido ignorada y Cicerón y los primeros matemáticos griegos atribuyeron erróneamente este teorema a Pitágoras.
Baudhayana también presentó una prueba geométrica usando triángulos isósceles, por lo que, para ser más precisos, atribuimos la prueba geométrica a Baudhayana y la prueba numérica (usando la teoría de números y el cálculo de áreas) a Apastamba. Además, otro antiguo matemático indio llamado Bhaskara proporcionó más tarde una prueba geométrica y numérica única que es conocida por el hecho de que es verdaderamente generalizada y funciona para todo tipo de triángulos y no es incongruente (no solo isósceles como en algunas pruebas más antiguas).
dando vueltas a la plaza
Otro problema abordado por Baudhayana es el de encontrar un círculo cuya área sea la misma que la de un cuadrado (lo contrario de la cuadratura del círculo). Su sutra i.58 da esta construcción:
Dibuja la mitad de su diagonal sobre el centro hacia la línea Este-Oeste; luego describe un círculo junto con una tercera parte de lo que está fuera del cuadrado.
raíz cuadrada de 2
Baudhayana i.61-2 (elaborado en Apastamba Sulbasūtra i.6) da la longitud de la diagonal de un cuadrado en términos de sus lados, lo que equivale a una fórmula para la raíz cuadrada de 2:
samasya dvikarani. pramanam trityena vardhayet
tac caturthenatmacatustrimsonena savisesah.
La diagonal [lit. “doblador”] de un cuadrado. La medida se incrementará en un tercio y en un cuarto disminuirá en el 34. Esa es su diagonal aproximadamente.
- La diagonal [lit. “doblador”] de un cuadrado. La medida se incrementará en un tercio y en un cuarto disminuirá en el 34. Esa es su diagonal aproximadamente.
Es decir,
que es correcto hasta cinco decimales.
Créditos: Wiki
Observación: Todas las imágenes, diseños o videos en esta página son propiedad de sus respectivos dueños. No poseemos estas imágenes/diseños/videos. Los recopilamos del motor de búsqueda y otras fuentes para usarlos como ideas para usted. No se pretende infringir los derechos de autor. Si tiene motivos para creer que uno de nuestros contenidos está violando sus derechos de autor, no tome ninguna acción legal ya que estamos tratando de difundir el conocimiento. Puede comunicarse con nosotros directamente para recibir un crédito o eliminar el artículo del sitio.