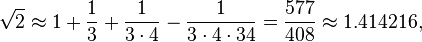జ్ఞానానికి మొట్టమొదటిది వేద గణితం. నిస్వార్థంగా హిందువులు ప్రపంచవ్యాప్తంగా పంచుకున్నారు. హిందూ తరచుగా అడిగే ప్రశ్నలు ఇప్పుడు ప్రపంచవ్యాప్తంగా కొన్ని ఆవిష్కరణలకు సమాధానం ఇస్తాయి, ఇవి వేదిక్ హిందుసింలో ఉండవచ్చు. మరియు నేను ఎప్పుడూ చెప్పినట్లుగా, మేము తీర్పు చెప్పలేము, మేము వ్యాసాన్ని వ్రాస్తాము, దానిని మీరు అంగీకరించాలా లేదా తిరస్కరించాలా అని తెలుసుకోవాలి. ఈ కథనాన్ని చదవడానికి మనకు ఓపెన్ మైండ్ అవసరం. మా నమ్మదగని చరిత్ర గురించి చదవండి మరియు తెలుసుకోండి. ఇది మీ మనస్సును చెదరగొడుతుంది! ! !
కానీ మొదట, స్టిగ్లెర్ యొక్క మారుపేరు యొక్క చట్టాన్ని నేను తెలియజేస్తాను:
"శాస్త్రీయ ఆవిష్కరణ దాని అసలు ఆవిష్కర్త పేరు పెట్టబడలేదు."
ఫన్నీ అది కాదు.
బాహలోని మరియు పైథాగరస్ లకు ముందు బాబిలోనియన్లు కుడి త్రిభుజం యొక్క నియమాన్ని తెలుసుకున్నారని మరియు ఉపయోగించారని కూడా చెప్పబడింది. ఇది యూక్లిడ్కు కొంతకాలం ముందు అభివృద్ధి చేయబడాలని కూడా ఉంది, మరియు ఇది యూక్లిడ్ యొక్క ఎలిమెంట్స్లో బాగా ప్రదర్శించబడుతుంది. ఇది ఎవరికైనా ముందు కనుగొన్నది చైనీస్ అని కొందరు పేర్కొన్నారు.
మొదట దాన్ని ఎవరు కనుగొన్నారో నేను వెళ్ళను, బదులుగా నేను బౌహాయనా సిద్ధాంతాన్ని వివరిస్తాను ఎందుకంటే మా వెబ్సైట్ హిందుయిజం గురించి తెలుసుకోవడం, మరియు హిందుయిజం ఎలా గొప్పదో నిరూపించటం కాదు.
కాబట్టి, బౌద్ధాయన, (క్రీ.పూ. 800) ధర్మ, రోజువారీ కర్మ, గణితం మొదలైనవాటిని వివరించే బౌద్ధాయన సూత్రాల రచయిత. అతను యజుర్వేద పాఠశాలకు చెందినవాడు, మరియు ఇతర సూత్ర రచయిత అపాస్తాంబ కంటే పెద్దవాడు.
బౌద్ధాయన సుల్బసూత్ర అని పిలువబడే బలిపీఠాల నిర్మాణానికి నియమాలు ఇచ్చే వేదాలకు తొలి సుల్బా సూత్ర అనుబంధాల రచయిత. గణితశాస్త్రం యొక్క కోణం నుండి ఇవి గుర్తించదగినవి, అనేక ముఖ్యమైన గణిత ఫలితాలను కలిగి ఉన్నాయి, వీటిలో పై విలువను కొంతవరకు ఖచ్చితత్వానికి ఇవ్వడం మరియు పైథాగరియన్ సిద్ధాంతం అని పిలువబడే సంస్కరణను పేర్కొనడం.

ఆదిమ పైథాగరియన్ ట్రిపుల్స్తో సంబంధం ఉన్న సీక్వెన్స్లకు బౌద్ధాయన సీక్వెన్స్లుగా పేరు పెట్టారు. ఈ సన్నివేశాలు గూ pt లిపి శాస్త్రంలో యాదృచ్ఛిక సన్నివేశాలుగా మరియు కీల తరం కొరకు ఉపయోగించబడ్డాయి.
పైథాగరస్ సిద్ధాంతం
లంబ కోణ త్రిభుజం యొక్క హైపోటెన్యూస్ యొక్క చతురస్రం ఇతర రెండు వైపుల చదరపు మొత్తానికి సమానం.
బౌద్ధాయన రాష్ట్రాలు:
“దీర్ఘచతురస్రం యొక్క వికర్ణం ద్వారా ఉత్పత్తి చేయబడిన ప్రాంతం రెండు వైపులా ఉత్పత్తి చేసిన విస్తీర్ణానికి సమానం.
బౌద్ధాయన తన పుస్తకంలో బౌద్ధాయన సుల్బసూత్ర (క్రీ.పూ. 800) అనే పైథాగరస్ సిద్ధాంతాన్ని జాబితా చేశాడు. యాదృచ్ఛికంగా, ఆధునిక గణితానికి సంబంధించిన పురాతన పుస్తకాలలో బౌద్ధాయన సుల్బసత్ర కూడా ఒకటి. పైథాగరస్ సిద్ధాంతాన్ని వివరించే బౌద్ధాయన సుల్బసూత్రలోని వాస్తవ శ్లోక (పద్యం) క్రింద ఇవ్వబడింది:
దీర్ఘస్యక్షణాయ రజ్జుh పార్శ్వమని, తిర్యాదం మణి,
చ యత్ప్రతాఘ్బుటే కురుతాస్తదుభయన్ కరోటి.
ఆసక్తికరంగా, పై శ్లోకాలో బౌద్ధాయన ఒక తాడును ఉదాహరణగా అనువదించవచ్చు - వికర్ణ పొడవు వెంట విస్తరించిన ఒక తాడు నిలువు మరియు క్షితిజ సమాంతర వైపులా కలిసి ఉండే ప్రాంతాన్ని ఉత్పత్తి చేస్తుంది. మీరు చూస్తున్నట్లుగా, పైథాగరస్ సిద్ధాంతాన్ని (మరియు సాధారణంగా జ్యామితిని) అర్థం చేసుకోవడానికి మరియు దృశ్యమానం చేయడానికి ఇది చాలా స్పష్టమైన మార్గం అని స్పష్టమవుతుంది మరియు బౌద్ధాయనా గణిత ఫలితాన్ని సాధారణ శ్లోకాలో సాధారణ వ్యక్తి భాషలో జతచేయడం ద్వారా అభ్యాస ప్రక్రియను సరళీకృతం చేసినట్లు అనిపిస్తుంది. .

కొంతమంది ఇది పైథాగరస్ సిద్ధాంతానికి అసలు గణిత రుజువు కాదని చెప్పవచ్చు మరియు పైథాగరస్ ఆ తప్పిపోయిన రుజువును అందించినట్లు తెలుస్తుంది. మేము అదే సుల్బసూత్రంలో చూస్తే, పైథాగరస్ సిద్ధాంతానికి రుజువును సుల్బా సూత్రాలలో బౌద్ధాయన మరియు అపాస్తాంబ రెండూ అందించినట్లు మనకు తెలుసు! విశదీకరించడానికి, శ్లోకను ఇలా అనువదించాలి -
దీర్ఘచతురస్రం యొక్క వికర్ణం దాని రెండు వైపులా విడిగా ఉత్పత్తి చేయబడిన రెండు (ప్రాంతాలు) స్వయంగా ఉత్పత్తి చేస్తుంది.
ఆధునిక పైథాగరియన్ సిద్ధాంతం
పై స్టేట్మెంట్ యొక్క చిక్కులు లోతైనవి ఎందుకంటే ఇది నేరుగా పైథాగరియన్ సిద్ధాంతంలోకి అనువదించబడింది మరియు బౌద్ధాయనా పైథాగరస్ సిద్ధాంతాన్ని రుజువు చేసినట్లు స్పష్టమవుతుంది. తరువాతి రుజువులు చాలావరకు రేఖాగణిత స్వభావం ఉన్నందున, సుల్బా సూత్రం యొక్క సంఖ్యా రుజువు దురదృష్టవశాత్తు విస్మరించబడింది. అయినప్పటికీ, పైథాగరియన్ ముగ్గులు మరియు రుజువులను అందించిన ఏకైక భారతీయ గణిత శాస్త్రజ్ఞుడు బౌద్ధాయన మాత్రమే కాదు.
పైథాగరస్ సిద్ధాంతానికి అపాస్టాంబా రుజువును కూడా అందించింది, ఇది మళ్ళీ సంఖ్యాపరంగా ఉంది, కానీ దురదృష్టవశాత్తు ఈ కీలకమైన సహకారం విస్మరించబడింది మరియు పైథాగరస్ ఈ సిద్ధాంతానికి సిసిరో మరియు ప్రారంభ గ్రీకు గణిత శాస్త్రవేత్తలచే తప్పుగా జమ చేయబడింది.
బౌద్ధాయన ఐసోసెల్ త్రిభుజాలను ఉపయోగించి రేఖాగణిత రుజువును కూడా సమర్పించారు, కాబట్టి మరింత ఖచ్చితంగా చెప్పాలంటే, మేము రేఖాగణిత రుజువును బౌద్ధాయనకు మరియు సంఖ్యాత్మక (సంఖ్య సిద్ధాంతం మరియు ప్రాంత గణనను ఉపయోగించి) రుజువును అపాస్టాంబకు ఆపాదించాము. అలాగే, మరొక పురాతన భారతీయ గణిత శాస్త్రజ్ఞుడు భాస్కర తరువాత ఒక ప్రత్యేకమైన రేఖాగణిత రుజువుతో పాటు సంఖ్యాపరంగా అందించాడు, ఇది నిజంగా సాధారణీకరించబడింది మరియు అన్ని రకాల త్రిభుజాల కోసం పనిచేస్తుంది మరియు అసంగతమైనది కాదు (కొన్ని పాత రుజువులలో ఉన్నట్లుగా ఐసోసెల్లే కాదు).
చదరపు చుట్టూ
బౌద్ధాయన చేత పరిష్కరించబడిన మరొక సమస్య ఏమిటంటే, ఒక వృత్తాన్ని కనుగొనడం, దీని వైశాల్యం చదరపు ప్రాంతానికి సమానంగా ఉంటుంది (వృత్తాన్ని స్క్వేర్ చేయడం యొక్క రివర్స్). అతని సూత్రం i.58 ఈ నిర్మాణాన్ని ఇస్తుంది:
తూర్పు-పడమర రేఖ వైపు మధ్యలో దాని వికర్ణంలో సగం గీయండి; అప్పుడు చదరపు వెలుపల ఉన్న మూడవ భాగంతో ఒక వృత్తాన్ని వివరించండి.
2 యొక్క వర్గమూలం
బౌద్ధాయనా i.61-2 (అపాస్టాంబ సుల్బాసత్ర i.6 లో వివరించబడింది) ఒక చదరపు వికర్ణ పొడవును దాని భుజాల పరంగా ఇస్తుంది, ఇది 2 యొక్క వర్గమూలానికి సూత్రానికి సమానం:
సమస్య ద్వికారాణి. ప్రమాణం తృత్యేన వర్ధయేత్
టాక్ కతుర్థేనాత్మకాటుస్త్రిమ్సోనేన సవిశేషah.
వికర్ణ [వెలిగిస్తారు. చదరపు “రెట్టింపు”]. కొలత మూడవ వంతు మరియు నాలుగవ వంతు 34 వ వంతు తగ్గుతుంది. దాని వికర్ణం సుమారు.
- వికర్ణ [వెలిగిస్తారు. చదరపు “రెట్టింపు”]. కొలత మూడవ వంతు మరియు నాలుగవ వంతు 34 వ వంతు తగ్గుతుంది. దాని వికర్ణం సుమారు.
అంటే,
ఇది ఐదు దశాంశాలకు సరైనది.
క్రెడిట్స్: వికీ
నిరాకరణ: ఈ పేజీలోని అన్ని చిత్రాలు, నమూనాలు లేదా వీడియోలు వాటి యజమానుల కాపీరైట్. ఈ చిత్రాలు / నమూనాలు / వీడియోలు మాకు లేవు. మీ కోసం ఆలోచనలుగా ఉపయోగించడానికి శోధన ఇంజిన్ మరియు ఇతర వనరుల నుండి మేము వాటిని సేకరిస్తాము. కాపీరైట్ ఉల్లంఘన ఉద్దేశించబడలేదు. మా కంటెంట్లో ఒకటి మీ కాపీరైట్లను ఉల్లంఘిస్తోందని మీకు నమ్మకం ఉంటే, దయచేసి మేము జ్ఞానాన్ని వ్యాప్తి చేయడానికి ప్రయత్నిస్తున్నందున చట్టపరమైన చర్యలు తీసుకోకండి. జమ చేయడానికి మీరు నేరుగా మమ్మల్ని సంప్రదించవచ్చు లేదా సైట్ నుండి అంశం తీసివేయబడవచ్చు.