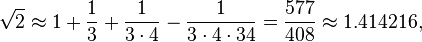વૈદિક ગણિત એ જ્ knowledgeાનનો પ્રથમ અને અગ્રણી સ્રોત હતો. નિlessસ્વાર્થ રીતે વિશ્વના તમામ હિન્દુઓ દ્વારા વહેંચાયેલું છે. હિન્દુ પ્રશ્નોત્તરીઓ હવે વિશ્વભરની કેટલીક શોધોનો જવાબ આપશે જે કદાચ વૈદિક હિંદુસીમમાં અસ્તિત્વ ધરાવે છે. અને હું હંમેશાં કહું છું કે, અમે ન્યાયાધીશ નહીં, અમે ફક્ત લેખ લખીશું, તે તમે છો કે જેને તે સ્વીકારવું કે નકારવું તે જાણવું જોઈએ. આપણે આ લેખ વાંચવા માટે ખુલ્લા મનની જરૂર છે. અમારા અવિશ્વસનીય ઇતિહાસ વિશે વાંચો અને જાણો. તે તમારા મગજમાં તમાચો આવશે! ! !

પરંતુ પહેલા, હું સ્ટીગલરનો મહાદેવના કાયદાને જણાવીશ:
"કોઈ વૈજ્ .ાનિક શોધ તેના મૂળ શોધકર્તાના નામ પર નથી."
રમુજી તે નથી.
ઠીક છે, એવો દાવો પણ કરવામાં આવે છે કે બાબેહૈના અને પાયથાગોરસથી ઘણા સમય પહેલા બેબીલોનના લોકો જમણા ત્રિકોણના નિયમને જાણતા હતા અને તેનો ઉપયોગ કરતા હતા. તે યુક્લિડના થોડા સમય પહેલાં વિકસિત થવાની પણ દાવેદાર છે, અને તે યુક્લિડના તત્વોમાં ખૂબ સારી રીતે પ્રદર્શિત થાય છે. કેટલાક દાવો કરે છે કે તે ચીની છે જેણે તેને બીજા કોઈની સમક્ષ શોધી કા .ી હતી.

ઠીક છે કે હું તેને પ્રથમ કોને અસ્વીકાર કરું તેની સાથે નહીં જઉં, બઉહૈનાની થિયરીને સમજાવું, કેમ કે અમારી વેબસાઇટ હિન્દુત્વ વિશે જાણવાની છે, અને હિન્દુત્વ કેવી રીતે સર્વશ્રેષ્ઠ છે તે સાબિત કરવું નહીં.

તેથી, બૌધ્યાન, (800 બીસીઇ) ધર્મ, દૈનિક ધાર્મિક વિધિ, ગણિત વગેરેને આવરી લેતા બૌધ્યાન સૂત્રોના લેખક હતા, તે યજુર્વેદ શાખાના છે, અને તે બીજા સૂત્ર લેખક આપસ્તમ્બા કરતા જુના છે.
તેઓ બૌધ્યાન સુલબાસૂત્ર તરીકે ઓળખાતી વેદીઓના નિયમો આપતા વેદમાં પ્રારંભિક સુલ્બા સૂત્ર પરિશિષ્ટના લેખક હતા. ગણિતના દ્રષ્ટિકોણથી આ નોંધપાત્ર છે, જેમાં કેટલાક મહત્વપૂર્ણ ગાણિતિક પરિણામો શામેલ છે, જેમાં કેટલાક અંશે ચોકસાઇ માટે પાઇનું મૂલ્ય આપવું, અને જેને પાયથાગોરિયન પ્રમેય તરીકે ઓળખવામાં આવે છે તેનું સંસ્કરણ જણાવવામાં આવે છે.

આદિકાળ પાયથાગોરિયન ત્રિવિધિઓ સાથે સંકળાયેલ સિક્વન્સને બૌધ્યાન ક્રમ નામ આપવામાં આવ્યું છે. આ સિક્વન્સ ક્રિપ્ટોગ્રાફીમાં રેન્ડમ સિક્વન્સ તરીકે અને કીઓના નિર્માણ માટે ઉપયોગમાં લેવાય છે.

પાયથાગોરિયન પ્રમેય
જમણા ખૂણાવાળા ત્રિકોણના પૂર્વધારણાનો વર્ગ અન્ય બે બાજુઓના વર્ગના સરખા જેટલો છે.

બૌધાયણ જણાવે છે:
“લંબચોરસના કર્ણ દ્વારા ઉત્પન્ન થયેલ ક્ષેત્ર તે બે બાજુએ દ્વારા ઉત્પાદિત ક્ષેત્રના સરવાળા જેટલું છે.

બૌધનાએ બૌધ્યાન સુલબાસુત્ર (800 બીસીઇ) નામના તેમના પુસ્તકમાં પાયથાગોરસ પ્રમેયની સૂચિબદ્ધ કરી. આકસ્મિક રીતે, બૌધ્યાન સુલ્બસત્ર એ અદ્યતન ગણિત પરના સૌથી પ્રાચીન પુસ્તકોમાંથી એક પણ છે. બૌધ્યાન સુલબાસુત્રમાં વાસ્તવિક શ્લોકા (શ્લોક) જે પાયથાગોરસ પ્રમેયનું વર્ણન કરે છે તે નીચે આપેલ છે:

દીર્ઘસ્યકસનાય રાજજુહ પાર્શ્વમાની, તિર્યાદમ મણિ,
ચ યત્પ્રથાગભૂતે કુરુસ્તસ્તદુભયં કરોતિ।

રસપ્રદ વાત એ છે કે બૌધનાએ ઉપરોક્ત શ્લોકામાં ઉદાહરણ તરીકે દોરાનો ઉપયોગ કર્યો જેનું ભાષાંતર કરી શકાય છે - કર્ણની લંબાઈ સાથે ખેંચાયેલ દોરડું એક ક્ષેત્ર પેદા કરે છે જે icalભી અને આડી બાજુ એકસાથે બનાવે છે. જેમ તમે જુઓ છો, તે સ્પષ્ટ થઈ ગયું છે કે પાયથાગોરસ પ્રમેય (અને સામાન્ય રીતે ભૂમિતિ) ને સમજવાની અને વિઝ્યુલાઇઝ કરવાની આ સૌથી અનુલક્ષી રીત છે અને બૌધ્યાને ગણિતકીય પરિણામને સામાન્ય માણસની ભાષામાં સરળ શ્લોકામાં સમાવીને શીખવાની પ્રક્રિયાને સરળ બનાવ્યું હોય તેવું લાગે છે. .

કેટલાક લોકો એમ કહી શકે છે કે આ પાયથાગોરસ પ્રમેયનો ખરેખર કોઈ ગણિતશાસ્ત્રીય પુરાવો નથી, અને શક્ય છે કે પાયથાગોરસએ તે ગુમ પુરાવો પૂરો પાડ્યો હતો. પરંતુ જો આપણે એ જ સુલબાસૂત્રમાં જોઈએ, તો આપણે શોધી કા !ીએ છીએ કે પાયથાગોરસ પ્રમેયનો પુરાવો બૌધ્યાન અને આપસ્તમ્બા બંનેએ સુલ્બા સૂત્રોમાં પૂરો પાડ્યો છે! વિસ્તૃત કરવા માટે, શ્લોકાનું ભાષાંતર આ પ્રમાણે કરવાનું છે -
એક લંબચોરસનું કર્ણ તેની બંને બાજુએ અલગથી ઉત્પાદિત બંને (ક્ષેત્ર) દ્વારા ઉત્પન્ન થાય છે.

આધુનિક પાયથાગોરિયન પ્રમેય
ઉપરોક્ત નિવેદનની અસરો ગહન છે કારણ કે તેનો સીધો પાયથાગોરિયન પ્રમેયમાં અનુવાદ કરવામાં આવે છે અને તે સ્પષ્ટ થાય છે કે બૌધાયને પાયથાગોરસ પ્રમેયને સાબિત કર્યું. પાછળના મોટાભાગના પુરાવા ભૌમિતિક સ્વભાવના હોવાથી, સુલબા સૂત્રના આંકડાકીય પુરાવા કમનસીબે અવગણવામાં આવ્યા હતા. તેમ છતાં, બૌધયાન એકમાત્ર ભારતીય ગણિતશાસ્ત્રી ન હતા જેમણે પાયથાગોરિયન ત્રિપુટીઓ અને પુરાવા પૂરા પાડ્યા હતા.

અપસ્તામ્બાએ પાયથાગોરસ પ્રમેય માટેનો પુરાવો પણ પૂરો પાડ્યો, જે ફરીથી પ્રકૃતિમાં આંકડાત્મક છે પરંતુ દુર્ભાગ્યવશ આ મહત્વપૂર્ણ યોગદાનની અવગણના કરવામાં આવી છે અને પાયથાગોરસને આ પ્રમેય માટે ખોટી રીતે સિસિરો અને પ્રારંભિક ગ્રીક ગણિતશાસ્ત્રીઓએ શ્રેય આપ્યો હતો.

બૌધનાએ આઇસોસેલ્સ ત્રિકોણનો ઉપયોગ કરીને ભૌમિતિક પુરાવો પણ રજૂ કર્યો, તેથી વધુ સચોટ હોવા માટે, આપણે ભૌમિતિક પુરાવાને બૌધયાન અને આંકડાકીય (નંબર સિદ્ધાંત અને ક્ષેત્રના ગણતરીનો ઉપયોગ કરીને) આપસ્તંભને પ્રસ્તુત કરીએ છીએ. ઉપરાંત, ભાસ્કરા નામના બીજા પ્રાચીન ભારતીય ગણિતશાસ્ત્રીએ પાછળથી એક અનોખું ભૌમિતિક પુરાવો તેમજ આંકડાકીય પૂરા પાડ્યા જે તે હકીકત માટે જાણીતા છે કે તે ખરેખર સામાન્યીકૃત છે અને તમામ પ્રકારના ત્રિકોણ માટે કામ કરે છે અને અસંગત નથી (કેટલાક જૂના પુરાવાઓની જેમ આઇસોસેલ્સ પણ નથી).

ચોરસ ચકરાવો

બૌધ્યાન દ્વારા સામનો કરવામાં આવતી બીજી સમસ્યા એ છે કે વર્તુળ શોધવાનું જેનું ક્ષેત્રફળ ચોરસ (વર્તુળના સ્ક્વેરિંગનું વિપરીત) જેવું જ છે. તેમનો સૂત્ર i.58 આ બાંધકામ આપે છે:

પૂર્વ-પશ્ચિમ લાઇન તરફના કેન્દ્ર વિશે તેની અડધી કર્ણ દોરો; પછી ચોરસની બહારના ભાગના ત્રીજા ભાગ સાથે એક વર્તુળનું વર્ણન કરો.

2 નો વર્ગમૂળ
બૌધના i.61-2 (આપસ્તમ્બા સુલબાસત્રા i.6 માં વિસ્તૃત) તેની બાજુઓની દ્રષ્ટિએ ચોરસની કર્ણની લંબાઈ આપે છે, જે 2 ના વર્ગમૂળના સૂત્રની સમકક્ષ છે:

સમાસ્ય દ્વિકર્ણી. પ્રણામં ત્રિત્યં વર્ધયેત્
તક કૈતુર્થેનાત્મકૃષ્ટ્રિમોસ્નેના સવિસીસah।

કર્ણ [સળગતું. ચોરસનું “બમણું”. માપ ત્રીજા દ્વારા અને ચોથા દ્વારા 34 મી દ્વારા ઘટાડવાનો છે. તે આશરે તેની વિકર્ણ છે.

કર્ણ [સળગતું. ચોરસનું “બમણું”. માપ ત્રીજા દ્વારા અને ચોથા દ્વારા 34 મી દ્વારા ઘટાડવાનો છે. તે આશરે તેની વિકર્ણ છે.

તે જ,

જે પાંચ દશાંશ સુધી યોગ્ય છે.

ક્રેડિટ્સ વિકિપીડિયા

પ્રાચીન ભારતીય યુએફઓ

જવાબદારીનો ઇનકાર: આ પૃષ્ઠની બધી છબીઓ, ડિઝાઇન અથવા વિડિઓઝ તેમના સંબંધિત માલિકોની ક copyrightપિરાઇટ છે. અમારી પાસે આ છબીઓ / ડિઝાઇન / વિડિઓ નથી. અમે તમારા માટે વિચારો તરીકે ઉપયોગ કરવા માટે શોધ એંજિન અને અન્ય સ્રોતમાંથી તેમને એકત્રિત કરીએ છીએ. કોઈ ક copyrightપિરાઇટનું ઉલ્લંઘન કરવાનો હેતુ નથી. જો તમને એવું માનવાનું કારણ છે કે અમારી એક સામગ્રી તમારા ક copyપિરાઇટનું ઉલ્લંઘન કરી રહી છે, તો કૃપા કરીને અમે કોઈ જ્ legalાન ફેલાવવાનો પ્રયાસ કરી રહ્યાં હોવાથી કોઈ કાનૂની પગલાં ન લો. તમે અમારો સીધો સંપર્ક કરવા માટે જમા થવા માટે અથવા સાઇટથી આઇટમ કા haveી શકો છો.