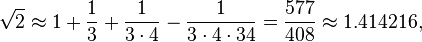Les mathématiques védiques étaient la première et la plus importante source de connaissances. Partagé de manière désintéressée par les hindous dans le monde entier. La FAQ hindoue répondra maintenant à certaines découvertes à travers le monde qui auraient pu exister chez les hindous védiques. Et comme je le dis toujours, nous ne jugerons pas, nous écrirons simplement l'article, c'est vous qui devriez savoir s'il faut l'accepter ou le rejeter. Nous avons besoin d'un esprit ouvert pour lire cet article. Lisez et découvrez notre incroyable histoire. Cela vous épatera! ! !
Mais d'abord, permettez-moi d'énoncer la loi d'éponymie de Stigler:
«Aucune découverte scientifique ne porte le nom de son découvreur d'origine.»
C'est drôle n'est-ce pas.
Eh bien, il est également affirmé que les Babyloniens connaissaient et utilisaient la règle du triangle rectangle bien avant Bauhayana et Pythagore. Il prétend également avoir été développé quelque temps avant Euclid, et il est très bien affiché dans Euclid's Elements. Certains prétendent que ce sont les Chinois qui l'ont découvert avant tout le monde.
Eh bien, je n'irai pas avec qui le découvre en premier, je voudrais plutôt expliquer la théorie de Bauhayana car notre site Web est de connaître l'hindouisme, et non de prouver comment l'hindouisme est le plus grand de tous.
Ainsi, Baudhayana, (800 avant notre ère) était l'auteur des sutras Baudhayana, qui couvrent le dharma, les rituels quotidiens, les mathématiques, etc. Il appartient à l'école Yajurveda et est plus âgé que l'autre auteur de sutra Apastamba.
Il était l'auteur des premiers appendices Sulba Sutra aux Vedas donnant des règles pour la construction d'autels appelés Baudhayana Sulbasutra. Celles-ci sont remarquables du point de vue des mathématiques, car elles contiennent plusieurs résultats mathématiques importants, notamment en donnant une valeur de pi avec un certain degré de précision et en énonçant une version de ce qui est maintenant connu sous le nom de théorème de Pythagore.

Les séquences associées aux triplets primitifs de Pythagore ont été nommées séquences Baudhayana. Ces séquences ont été utilisées en cryptographie comme séquences aléatoires et pour la génération de clés.
Théorème de Pythagore
Le carré de l'hypoténuse d'un triangle rectangle est égal à la somme du carré des deux autres côtés.
États Baudhayana:
«L'aire produite par la diagonale d'un rectangle est égale à la somme d'aire produite par celui-ci sur deux côtés.
Baudhayana a énuméré le théorème de Pythagore dans son livre intitulé Baudhayana Sulbasutra (800 BCE). Soit dit en passant, Baudhayana Sulbasûtra est également l'un des plus anciens livres sur les mathématiques avancées. Le shloka réel (verset) dans Baudhayana Sulbasutra qui décrit le théorème de Pythagore est donné ci-dessous:
dirghasyaksanaya rajjuh parsvamani, tiryadam mani,
cha yatprthagbhute kurutastadubhayan karoti.
Fait intéressant, Baudhayana a utilisé une corde comme exemple dans le shloka ci-dessus qui peut être traduit par - Une corde tendue le long de la diagonale produit une zone que les côtés verticaux et horizontaux forment ensemble. Comme vous le voyez, il devient clair que c'est peut-être la manière la plus intuitive de comprendre et de visualiser le théorème de Pythagore (et la géométrie en général) et Baudhāyana semble avoir simplifié le processus d'apprentissage en encapsulant le résultat mathématique dans un simple shloka dans un langage profane. .

Certaines personnes pourraient dire que ce n'est pas vraiment une preuve mathématique réelle du théorème de Pythagore et il est possible que Pythagore ait fourni cette preuve manquante. Mais si nous regardons dans le même Sulbasutra, nous constatons que la preuve du théorème de Pythagore a été fournie à la fois par Baudhayana et Apastamba dans les Sulba Sutras! Pour élaborer, le shloka doit être traduit par -
La diagonale d'un rectangle produit par elle-même les deux (les zones) produites séparément par ses deux côtés.
Théorème de Pythagore moderne
Les implications de la déclaration ci-dessus sont profondes car elle est directement traduite en théorème de Pythagore et il devient évident que Baudhayana a prouvé le théorème de Pythagore. Étant donné que la plupart des preuves ultérieures sont de nature géométrique, la preuve numérique du Sulba Sutra a malheureusement été ignorée. Cependant, Baudhayana n'était pas le seul mathématicien indien à avoir fourni des triplés et des preuves de Pythagore.
Apastamba a également fourni la preuve du théorème de Pythagore, qui est à nouveau de nature numérique, mais encore une fois, malheureusement, cette contribution vitale a été ignorée et Pythagore a été à tort crédité par Cicéron et les premiers mathématiciens grecs pour ce théorème.
Baudhayana a également présenté une preuve géométrique utilisant des triangles isocèles, donc, pour être plus précis, nous attribuons la preuve géométrique à Baudhayana et la preuve numérique (en utilisant la théorie des nombres et le calcul des aires) à Apastamba. En outre, un autre mathématicien indien ancien appelé Bhaskara a fourni plus tard une preuve géométrique unique ainsi que numérique, connue pour le fait qu'elle est vraiment généralisée et fonctionne pour toutes sortes de triangles et qu'elle n'est pas incongrue (pas seulement isocèle comme dans certaines preuves plus anciennes).
Faire le tour de la place
Un autre problème abordé par Baudhayana est celui de trouver un cercle dont l'aire est la même que celle d'un carré (l'inverse de la quadrature du cercle). Son sutra i.58 donne cette construction:
Tracez la moitié de sa diagonale autour du centre vers la ligne Est-Ouest; puis décrivez un cercle avec une troisième partie de ce qui se trouve à l'extérieur du carré.
Racine carrée de 2
Baudhayana i.61-2 (élaboré dans Apastamba Sulbasūtra i.6) donne la longueur de la diagonale d'un carré en fonction de ses côtés, ce qui équivaut à une formule pour la racine carrée de 2:
samasya dvikarani. Pramanam Trityena Vardhayet
tac caturthenatmacatustrimsonena savisesah.
La diagonale [lit. «Doubleur»] d'un carré. La mesure doit être augmentée d'un tiers et d'un quart diminuée du 34ème. C'est sa diagonale approximativement.
- La diagonale [lit. «Doubleur»] d'un carré. La mesure doit être augmentée d'un tiers et d'un quart diminuée du 34ème. C'est sa diagonale approximativement.
Autrement dit,
ce qui est correct à cinq décimales.
Crédits: Wiki
Clause de non-responsabilité : Toutes les images, dessins ou vidéos de cette page sont la propriété de leurs propriétaires respectifs. Nous ne possédons pas ces images / dessins / vidéos. Nous les collectons à partir des moteurs de recherche et d'autres sources pour être utilisés comme idées pour vous. Aucune violation du droit d'auteur n'est prévue. Si vous avez des raisons de croire que l'un de nos contenus enfreint vos droits d'auteur, veuillez ne pas engager de poursuites judiciaires car nous essayons de diffuser les connaissances. Vous pouvez nous contacter directement pour être crédité ou faire retirer l'article du site.