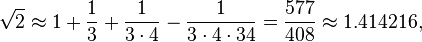ವೈದಿಕ ಗಣಿತವು ಜ್ಞಾನದ ಮೊದಲ ಮತ್ತು ಪ್ರಮುಖ ಮೂಲವಾಗಿತ್ತು. ನಿಸ್ವಾರ್ಥವಾಗಿ ಹಿಂದೂಗಳು ಪ್ರಪಂಚದಾದ್ಯಂತ ಹಂಚಿಕೊಂಡಿದ್ದಾರೆ. ಹಿಂದೂ FAQ ಗಳು ಈಗ ಪ್ರಪಂಚದಾದ್ಯಂತದ ಕೆಲವು ಆವಿಷ್ಕಾರಗಳಿಗೆ ಉತ್ತರಿಸುತ್ತವೆ, ಅದು ವೇದ ಹಿಂದೂಸಿಮ್ನಲ್ಲಿ ಅಸ್ತಿತ್ವದಲ್ಲಿರಬಹುದು. ಮತ್ತು ನಾನು ಯಾವಾಗಲೂ ಹೇಳುವಂತೆ, ನಾವು ನಿರ್ಣಯಿಸುವುದಿಲ್ಲ, ನಾವು ಲೇಖನವನ್ನು ಬರೆಯುತ್ತೇವೆ, ಅದನ್ನು ಸ್ವೀಕರಿಸಬೇಕೆ ಅಥವಾ ತಿರಸ್ಕರಿಸಬೇಕೆ ಎಂದು ನೀವು ತಿಳಿದುಕೊಳ್ಳಬೇಕು. ಈ ಲೇಖನವನ್ನು ಓದಲು ನಮಗೆ ಮುಕ್ತ ಮನಸ್ಸು ಬೇಕು. ನಮ್ಮ ನಂಬಲಾಗದ ಇತಿಹಾಸದ ಬಗ್ಗೆ ಓದಿ ಮತ್ತು ಕಲಿಯಿರಿ. ಅದು ನಿಮ್ಮ ಮನಸ್ಸನ್ನು ಸ್ಫೋಟಿಸುತ್ತದೆ! ! !
ಆದರೆ ಮೊದಲು, ಸ್ಟಿಗ್ಲರ್ನ ನಾಮಸೂಚಕ ನಿಯಮವನ್ನು ನಾನು ಹೇಳುತ್ತೇನೆ:
"ಯಾವುದೇ ವೈಜ್ಞಾನಿಕ ಆವಿಷ್ಕಾರವನ್ನು ಅದರ ಮೂಲ ಅನ್ವೇಷಕನ ಹೆಸರಿಡಲಾಗಿಲ್ಲ."
ತಮಾಷೆಯಲ್ಲ.
ಬೌಹಾಯಾನ ಮತ್ತು ಪೈಥಾಗರಸ್ಗೆ ಬಹಳ ಹಿಂದೆಯೇ ಬ್ಯಾಬಿಲೋನಿಯನ್ನರು ಸರಿಯಾದ ತ್ರಿಕೋನದ ನಿಯಮವನ್ನು ತಿಳಿದಿದ್ದರು ಮತ್ತು ಬಳಸಿದ್ದಾರೆಂದು ಹೇಳಲಾಗಿದೆ. ಇದು ಯೂಕ್ಲಿಡ್ಗೆ ಸ್ವಲ್ಪ ಸಮಯದ ಮೊದಲು ಅಭಿವೃದ್ಧಿಪಡಿಸಲಾಗುವುದು ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ, ಮತ್ತು ಇದನ್ನು ಯೂಕ್ಲಿಡ್ಸ್ ಎಲಿಮೆಂಟ್ಸ್ನಲ್ಲಿ ಚೆನ್ನಾಗಿ ಪ್ರದರ್ಶಿಸಲಾಗುತ್ತದೆ. ಇದನ್ನು ಚೈನೀಸ್ ಎಂದು ಬೇರೆಯವರ ಮುಂದೆ ಕಂಡುಹಿಡಿದಿದ್ದಾರೆ ಎಂದು ಕೆಲವರು ಹೇಳುತ್ತಾರೆ.
ಮೊದಲಿಗೆ ಅದನ್ನು ಕಂಡುಹಿಡಿದವರೊಂದಿಗೆ ನಾನು ಹೋಗುವುದಿಲ್ಲ, ಬದಲಿಗೆ ನಾನು ಬೌಹಾಯನ ಸಿದ್ಧಾಂತವನ್ನು ವಿವರಿಸುತ್ತೇನೆ ಏಕೆಂದರೆ ನಮ್ಮ ವೆಬ್ಸೈಟ್ ಹಿಂದೂ ಧರ್ಮದ ಬಗ್ಗೆ ತಿಳಿದುಕೊಳ್ಳುವುದು, ಮತ್ತು ಹಿಂದೂ ಧರ್ಮವನ್ನು ಹೇಗೆ ಶ್ರೇಷ್ಠವೆಂದು ಸಾಬೀತುಪಡಿಸುವುದು ಎಲ್ಲಕ್ಕಿಂತ ದೊಡ್ಡದು.
ಆದ್ದರಿಂದ, ಬೌದ್ಧಾಯಣ, (ಕ್ರಿ.ಪೂ 800) ಧರ್ಮ, ದೈನಂದಿನ ಆಚರಣೆ, ಗಣಿತ ಇತ್ಯಾದಿಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಬೌದ್ಧಾಯನ ಸೂತ್ರಗಳ ಲೇಖಕರಾಗಿದ್ದರು. ಅವರು ಯಜುರ್ವೇದ ಶಾಲೆಗೆ ಸೇರಿದವರಾಗಿದ್ದಾರೆ ಮತ್ತು ಇತರ ಸೂತ್ರ ಲೇಖಕ ಅಪಸ್ತಂಬರಿಗಿಂತ ಹಿರಿಯರು.
ಬೌದ್ಧಾಯನ ಸುಲ್ಬಸೂತ್ರ ಎಂಬ ಬಲಿಪೀಠಗಳ ನಿರ್ಮಾಣಕ್ಕೆ ನಿಯಮಗಳನ್ನು ನೀಡುವ ವೇದಗಳಿಗೆ ಆರಂಭಿಕ ಸುಲ್ಬಾ ಸೂತ್ರದ ಅನುಬಂಧಗಳ ಲೇಖಕರಾಗಿದ್ದರು. ಗಣಿತದ ದೃಷ್ಟಿಕೋನದಿಂದ ಇವು ಗಮನಾರ್ಹವಾಗಿವೆ, ಹಲವಾರು ಪ್ರಮುಖ ಗಣಿತದ ಫಲಿತಾಂಶಗಳನ್ನು ಒಳಗೊಂಡಿವೆ, ಇದರಲ್ಲಿ ಪೈ ಮೌಲ್ಯವನ್ನು ಸ್ವಲ್ಪ ಮಟ್ಟಿಗೆ ನಿಖರವಾಗಿ ನೀಡುವುದು, ಮತ್ತು ಈಗ ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯ ಎಂದು ಕರೆಯಲ್ಪಡುವ ಆವೃತ್ತಿಯನ್ನು ಹೇಳುವುದು.

ಪ್ರಾಚೀನ ಪೈಥಾಗರಿಯನ್ ತ್ರಿವಳಿಗಳಿಗೆ ಸಂಬಂಧಿಸಿದ ಅನುಕ್ರಮಗಳನ್ನು ಬೌದ್ಧಾಯನ ಅನುಕ್ರಮಗಳು ಎಂದು ಹೆಸರಿಸಲಾಗಿದೆ. ಈ ಅನುಕ್ರಮಗಳನ್ನು ಗುಪ್ತ ಲಿಪಿ ಶಾಸ್ತ್ರದಲ್ಲಿ ಯಾದೃಚ್ sequ ಿಕ ಅನುಕ್ರಮಗಳಾಗಿ ಮತ್ತು ಕೀಗಳ ಉತ್ಪಾದನೆಗೆ ಬಳಸಲಾಗುತ್ತದೆ.
ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯ
ಲಂಬ-ಕೋನ ತ್ರಿಕೋನದ ಹೈಪೋಟೆನ್ಯೂಸ್ನ ಚೌಕವು ಇತರ ಎರಡು ಬದಿಗಳ ಚೌಕದ ಮೊತ್ತಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ.
ಬೌದ್ಧಾಯನ ರಾಜ್ಯಗಳು:
“ಒಂದು ಆಯತದ ಕರ್ಣದಿಂದ ಉತ್ಪತ್ತಿಯಾಗುವ ಪ್ರದೇಶವು ಎರಡು ಬದಿಗಳಲ್ಲಿ ಉತ್ಪತ್ತಿಯಾಗುವ ಪ್ರದೇಶದ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
ಬೌದ್ಧಾಯನ ತನ್ನ ಪುಸ್ತಕದಲ್ಲಿ ಬೌದ್ಧಾಯನ ಸುಲ್ಬಸೂತ್ರ (ಕ್ರಿ.ಪೂ 800) ಎಂಬ ಪೈಥಾಗರಸ್ ಪ್ರಮೇಯವನ್ನು ಪಟ್ಟಿಮಾಡಿದ್ದಾನೆ. ಪ್ರಾಸಂಗಿಕವಾಗಿ, ಬೌದ್ಧಾಯನ ಸುಲ್ಬಾಸತ್ರವು ಸುಧಾರಿತ ಗಣಿತಶಾಸ್ತ್ರದ ಅತ್ಯಂತ ಹಳೆಯ ಪುಸ್ತಕಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ. ಪೈಥಾಗರಸ್ ಪ್ರಮೇಯವನ್ನು ವಿವರಿಸುವ ಬೌದ್ಧಾಯನ ಸುಲ್ಬಸೂತ್ರದಲ್ಲಿನ ನಿಜವಾದ ಶ್ಲೋಕ (ಪದ್ಯ) ಕೆಳಗೆ ನೀಡಲಾಗಿದೆ:
ದೀರ್ಘಸ್ಯಕ್ಷಣಾಯ ರಜ್ಜುಃ ಪಾರ್ಶ್ವಮಣಿ, ತಿರ್ಯದಂ ಮಣಿ,
ಚ ಯತ್ಪ್ರತಘುತು ಕುರುತಸ್ತದುಭಯನ್ ಕರೋಟಿ.
ಕುತೂಹಲಕಾರಿಯಾಗಿ, ಮೇಲಿನ ಶ್ಲೋಕದಲ್ಲಿ ಬೌದ್ಧಾಯಣವು ಒಂದು ಹಗ್ಗವನ್ನು ಉದಾಹರಣೆಯಾಗಿ ಬಳಸಿದೆ - ಇದನ್ನು ಕರ್ಣೀಯ ಉದ್ದಕ್ಕೂ ವಿಸ್ತರಿಸಿರುವ ಹಗ್ಗವು ಲಂಬ ಮತ್ತು ಅಡ್ಡ ಬದಿಗಳು ಒಟ್ಟಿಗೆ ಮಾಡುವ ಪ್ರದೇಶವನ್ನು ಉತ್ಪಾದಿಸುತ್ತದೆ. ನೀವು ನೋಡುವಂತೆ, ಇದು ಬಹುಶಃ ಪೈಥಾಗರಸ್ ಪ್ರಮೇಯವನ್ನು (ಮತ್ತು ಸಾಮಾನ್ಯವಾಗಿ ಜ್ಯಾಮಿತಿಯನ್ನು) ಅರ್ಥಮಾಡಿಕೊಳ್ಳುವ ಮತ್ತು ದೃಶ್ಯೀಕರಿಸುವ ಅತ್ಯಂತ ಅರ್ಥಗರ್ಭಿತ ಮಾರ್ಗವಾಗಿದೆ ಮತ್ತು ಬೌದ್ಧಾನ ಗಣಿತದ ಫಲಿತಾಂಶವನ್ನು ಸಾಮಾನ್ಯ ಶ್ಲೋಕದಲ್ಲಿ ಸಾಮಾನ್ಯ ವ್ಯಕ್ತಿಯ ಭಾಷೆಯಲ್ಲಿ ಸುತ್ತುವರಿಯುವ ಮೂಲಕ ಕಲಿಕೆಯ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಸರಳೀಕರಿಸಿದಂತೆ ತೋರುತ್ತದೆ. .

ಇದು ನಿಜವಾಗಿಯೂ ಪೈಥಾಗರಸ್ ಪ್ರಮೇಯದ ನಿಜವಾದ ಗಣಿತದ ಪುರಾವೆಯಲ್ಲ ಎಂದು ಕೆಲವರು ಹೇಳಬಹುದು ಮತ್ತು ಪೈಥಾಗರಸ್ ಆ ಕಾಣೆಯಾದ ಪುರಾವೆಗಳನ್ನು ಒದಗಿಸಿರಬಹುದು. ಆದರೆ ನಾವು ಒಂದೇ ಸುಲ್ಬಸೂತ್ರದಲ್ಲಿ ನೋಡಿದರೆ, ಪೈಥಾಗರಸ್ ಪ್ರಮೇಯದ ಪುರಾವೆಗಳನ್ನು ಬೌಲ್ಯಾಯನ ಮತ್ತು ಅಪಸ್ತಂಬಾ ಇಬ್ಬರೂ ಸುಲ್ಬಾ ಸೂತ್ರಗಳಲ್ಲಿ ಒದಗಿಸಿದ್ದಾರೆ ಎಂದು ನಾವು ಕಂಡುಕೊಂಡಿದ್ದೇವೆ! ವಿಸ್ತಾರವಾಗಿ ಹೇಳುವುದಾದರೆ, ಶ್ಲೋಕವನ್ನು ಹೀಗೆ ಅನುವಾದಿಸಬೇಕು -
ಒಂದು ಆಯತದ ಕರ್ಣವು ಅದರ ಎರಡು ಬದಿಗಳಿಂದ ಪ್ರತ್ಯೇಕವಾಗಿ ಉತ್ಪತ್ತಿಯಾಗುವ ಎರಡೂ (ಪ್ರದೇಶಗಳು) ಸ್ವತಃ ಉತ್ಪಾದಿಸುತ್ತದೆ.
ಆಧುನಿಕ ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯ
ಮೇಲಿನ ಹೇಳಿಕೆಯ ಪರಿಣಾಮಗಳು ಗಾ are ವಾಗಿವೆ ಏಕೆಂದರೆ ಇದನ್ನು ನೇರವಾಗಿ ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯಕ್ಕೆ ಅನುವಾದಿಸಲಾಗಿದೆ ಮತ್ತು ಬೌದ್ಧಾಯನ ಪೈಥಾಗರಸ್ ಪ್ರಮೇಯವನ್ನು ಸಾಬೀತುಪಡಿಸಿದನೆಂದು ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ. ನಂತರದ ಹೆಚ್ಚಿನ ಪುರಾವೆಗಳು ಜ್ಯಾಮಿತೀಯ ಸ್ವರೂಪದಲ್ಲಿರುವುದರಿಂದ, ಸುಲ್ಬಾ ಸೂತ್ರದ ಸಂಖ್ಯಾತ್ಮಕ ಪುರಾವೆಗಳನ್ನು ದುರದೃಷ್ಟವಶಾತ್ ನಿರ್ಲಕ್ಷಿಸಲಾಗಿದೆ. ಆದರೂ, ಪೈಥಾಗರಿಯನ್ ತ್ರಿವಳಿ ಮತ್ತು ಪುರಾವೆಗಳನ್ನು ಒದಗಿಸಿದ ಏಕೈಕ ಭಾರತೀಯ ಗಣಿತಜ್ಞ ಬೌದ್ಧಾಯನ ಮಾತ್ರವಲ್ಲ.
ಪೈಥಾಗರಸ್ ಪ್ರಮೇಯಕ್ಕೆ ಅಪಸ್ತಂಬಾ ಸಹ ಪುರಾವೆಗಳನ್ನು ಒದಗಿಸಿದೆ, ಅದು ಮತ್ತೆ ಸಂಖ್ಯಾತ್ಮಕವಾಗಿದೆ ಆದರೆ ಮತ್ತೆ ದುರದೃಷ್ಟವಶಾತ್ ಈ ಮಹತ್ವದ ಕೊಡುಗೆಯನ್ನು ನಿರ್ಲಕ್ಷಿಸಲಾಗಿದೆ ಮತ್ತು ಪೈಥಾಗರಸ್ ಅನ್ನು ಸಿಸೆರೊ ಮತ್ತು ಆರಂಭಿಕ ಗ್ರೀಕ್ ಗಣಿತಜ್ಞರು ಈ ಪ್ರಮೇಯಕ್ಕೆ ತಪ್ಪಾಗಿ ಸಲ್ಲುತ್ತಾರೆ.
ಬೌದ್ಧಾಯನ ಐಸೊಸೆಲ್ಸ್ ತ್ರಿಕೋನಗಳನ್ನು ಬಳಸಿಕೊಂಡು ಜ್ಯಾಮಿತೀಯ ಪುರಾವೆಗಳನ್ನು ಸಹ ಪ್ರಸ್ತುತಪಡಿಸಿದೆ, ಆದ್ದರಿಂದ ಹೆಚ್ಚು ನಿಖರವಾಗಿ ಹೇಳಬೇಕೆಂದರೆ, ನಾವು ಜ್ಯಾಮಿತೀಯ ಪುರಾವೆಗಳನ್ನು ಬೌದ್ಧಾಯಣಕ್ಕೆ ಮತ್ತು ಸಂಖ್ಯಾತ್ಮಕ (ಸಂಖ್ಯೆ ಸಿದ್ಧಾಂತ ಮತ್ತು ಪ್ರದೇಶ ಗಣನೆಯನ್ನು ಬಳಸಿ) ಪುರಾವೆಗಳನ್ನು ಅಪಸ್ತಂಬಾಗೆ ಆರೋಪಿಸುತ್ತೇವೆ. ಅಲ್ಲದೆ, ಭಾಸ್ಕರ ಎಂಬ ಇನ್ನೊಬ್ಬ ಪ್ರಾಚೀನ ಭಾರತೀಯ ಗಣಿತಜ್ಞನು ನಂತರ ಒಂದು ವಿಶಿಷ್ಟವಾದ ಜ್ಯಾಮಿತೀಯ ಪುರಾವೆ ಮತ್ತು ಸಂಖ್ಯಾತ್ಮಕತೆಯನ್ನು ಒದಗಿಸಿದನು, ಇದು ನಿಜಕ್ಕೂ ಸಾಮಾನ್ಯೀಕರಿಸಲ್ಪಟ್ಟಿದೆ ಮತ್ತು ಎಲ್ಲಾ ರೀತಿಯ ತ್ರಿಕೋನಗಳಿಗೆ ಕೆಲಸ ಮಾಡುತ್ತದೆ ಮತ್ತು ಅಸಂಗತವಲ್ಲ (ಕೆಲವು ಹಳೆಯ ಪುರಾವೆಗಳಂತೆ ಐಸೊಸೆಲ್ಗಳು ಮಾತ್ರವಲ್ಲ).
ಚೌಕವನ್ನು ಸುತ್ತುತ್ತದೆ
ಬೌದ್ಧಾಯನ ನಿಭಾಯಿಸಿದ ಮತ್ತೊಂದು ಸಮಸ್ಯೆ ಎಂದರೆ, ಅದರ ಪ್ರದೇಶವು ಚೌಕದ ಪ್ರದೇಶಕ್ಕೆ ಸಮನಾಗಿರುವ ವೃತ್ತವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು (ವೃತ್ತವನ್ನು ವರ್ಗೀಕರಿಸುವ ಹಿಮ್ಮುಖ). ಅವರ ಸೂತ್ರ i.58 ಈ ನಿರ್ಮಾಣವನ್ನು ನೀಡುತ್ತದೆ:
ಪೂರ್ವ-ಪಶ್ಚಿಮ ರೇಖೆಯ ಕಡೆಗೆ ಕೇಂದ್ರದ ಅರ್ಧದಷ್ಟು ಕರ್ಣವನ್ನು ಎಳೆಯಿರಿ; ನಂತರ ಚೌಕದ ಹೊರಗೆ ಇರುವ ಮೂರನೇ ಭಾಗದೊಂದಿಗೆ ವೃತ್ತವನ್ನು ವಿವರಿಸಿ.
2 ರ ವರ್ಗಮೂಲ
ಬೌದ್ಧಾಯನ i.61-2 (ಅಪಸ್ತಂಬಾ ಸುಲ್ಬಾಸತ್ರ i.6 ರಲ್ಲಿ ವಿವರಿಸಲಾಗಿದೆ) ಒಂದು ಚೌಕದ ಕರ್ಣೀಯ ಉದ್ದವನ್ನು ಅದರ ಬದಿಗಳಿಗೆ ಅನುಗುಣವಾಗಿ ನೀಡುತ್ತದೆ, ಇದು 2 ರ ವರ್ಗಮೂಲಕ್ಕೆ ಸೂತ್ರಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ:
ಸಮಸ್ಯ ದ್ವಿಕಾರಾಣಿ. ಪ್ರಮಾಣಂ ತೃತ್ಯೇನ ವರ್ಧಯೇತ್
ಟಾಕ್ ಕತುರ್ಥೇನಾತ್ಮಕಾತುಸ್ಟ್ರಿಮ್ಸೋನೇನ ಸವಿಸೇಸಃ.
ಕರ್ಣ [ಲಿಟ್. ಚೌಕದ “ದ್ವಿಗುಣ”]. ಅಳತೆಯನ್ನು ಮೂರನೆಯದರಿಂದ ಮತ್ತು ನಾಲ್ಕನೆಯದನ್ನು 34 ನೇಯಿಂದ ಕಡಿಮೆಗೊಳಿಸಬೇಕು. ಅದು ಸರಿಸುಮಾರು ಅದರ ಕರ್ಣೀಯವಾಗಿದೆ.
- ಕರ್ಣ [ಲಿಟ್. ಚೌಕದ “ದ್ವಿಗುಣ”]. ಅಳತೆಯನ್ನು ಮೂರನೆಯದರಿಂದ ಮತ್ತು ನಾಲ್ಕನೆಯದನ್ನು 34 ನೇಯಿಂದ ಕಡಿಮೆಗೊಳಿಸಬೇಕು. ಅದು ಸರಿಸುಮಾರು ಅದರ ಕರ್ಣೀಯವಾಗಿದೆ.
ಅದು,
ಇದು ಐದು ದಶಮಾಂಶಗಳಿಗೆ ಸರಿಯಾಗಿದೆ.
ಕ್ರೆಡಿಟ್ಸ್: ವಿಕಿ
ಹಕ್ಕುತ್ಯಾಗ: ಈ ಪುಟದಲ್ಲಿನ ಎಲ್ಲಾ ಚಿತ್ರಗಳು, ವಿನ್ಯಾಸಗಳು ಅಥವಾ ವೀಡಿಯೊಗಳು ಆಯಾ ಮಾಲೀಕರ ಹಕ್ಕುಸ್ವಾಮ್ಯ. ಈ ಚಿತ್ರಗಳು / ವಿನ್ಯಾಸಗಳು / ವೀಡಿಯೊಗಳನ್ನು ನಾವು ಹೊಂದಿಲ್ಲ. ನಿಮಗಾಗಿ ಆಲೋಚನೆಗಳಾಗಿ ಬಳಸಲು ನಾವು ಅವುಗಳನ್ನು ಸರ್ಚ್ ಎಂಜಿನ್ ಮತ್ತು ಇತರ ಮೂಲಗಳಿಂದ ಸಂಗ್ರಹಿಸುತ್ತೇವೆ. ಯಾವುದೇ ಹಕ್ಕುಸ್ವಾಮ್ಯ ಉಲ್ಲಂಘನೆಯನ್ನು ಉದ್ದೇಶಿಸಿಲ್ಲ. ನಮ್ಮ ವಿಷಯವು ನಿಮ್ಮ ಹಕ್ಕುಸ್ವಾಮ್ಯಗಳನ್ನು ಉಲ್ಲಂಘಿಸುತ್ತಿದೆ ಎಂದು ನಂಬಲು ನಿಮಗೆ ಕಾರಣವಿದ್ದರೆ, ದಯವಿಟ್ಟು ನಾವು ಜ್ಞಾನವನ್ನು ಹರಡಲು ಪ್ರಯತ್ನಿಸುತ್ತಿರುವುದರಿಂದ ಯಾವುದೇ ಕಾನೂನು ಕ್ರಮ ತೆಗೆದುಕೊಳ್ಳಬೇಡಿ. ಮನ್ನಣೆ ಪಡೆಯಲು ನೀವು ನೇರವಾಗಿ ನಮ್ಮನ್ನು ಸಂಪರ್ಕಿಸಬಹುದು ಅಥವಾ ಸೈಟ್ನಿಂದ ಐಟಂ ಅನ್ನು ತೆಗೆದುಹಾಕಬಹುದು.